Les arbres Merkle sont un composant fondamental des blockchains qui sous-tendent leur fonctionnalité. Ils permettent une vérification efficace et sécurisée des grandes structures de données et, dans le cas des blockchains, des ensembles de données potentiellement illimités.
L’implémentation d’arbres Merkle dans les blockchains a de multiples effets. Cela leur permet d’évoluer tout en leur fournissant une architecture basée sur le hachage pour maintenir l’intégrité des données et un moyen simple de vérifier l’intégrité des données..
Les fonctions de hachage cryptographique sont la technologie sous-jacente qui permet aux arbres Merkle de fonctionner, il est donc important de comprendre d’abord ce que sont les fonctions de hachage cryptographiques..
Fonctions de hachage cryptographique
En termes simples, une fonction de hachage est toute fonction utilisée pour mapper des données d’une taille arbitraire (entrée) à une sortie de taille fixe. Un algorithme de hachage est appliqué à l’entrée de données et la sortie de longueur fixe résultante est appelée hachage.
De nombreux algorithmes de hachage sont largement accessibles au public et peuvent être sélectionnés en fonction de vos besoins.
Le hachage résultant de l’entrée arbitraire n’est pas seulement fixe en longueur, il est également complètement unique à l’entrée et la fonction elle-même est déterministe. Autrement dit, peu importe le nombre de fois que vous exécutez la fonction sur la même entrée, la sortie sera toujours la même.
Par exemple, si vous avez les ensembles de données suivants ci-dessous en tant qu’entrée, les sorties résultantes sont uniques pour chaque entrée. Remarquez comment dans les deuxième et troisième exemples, même si la différence des entrées est d’un seul mot, les sorties résultantes sont complètement différentes.
Ceci est très important car cela permet une «empreinte digitale» des données.
Une fonction de hachage cryptographique, Image de Wikipédia
Étant donné que la longueur de sortie (somme de hachage dans l’exemple) est toujours la même que celle déterminée par l’algorithme de hachage utilisé, d’énormes quantités de données peuvent être identifiées uniquement grâce à leur hachage résultant.
Avec des systèmes qui contiennent d’énormes quantités de données, les avantages de pouvoir stocker et identifier les données avec une sortie de longueur fixe peuvent créer de vastes économies de stockage et contribuer à accroître l’efficacité..
Dans les blockchains, des algorithmes de hachage sont utilisés pour déterminer l’état de la blockchain.
Les blockchains sont des listes liées qui contiennent des données et un pointeur de hachage qui pointe vers le bloc précédent, créant une chaîne de blocs connectés, d’où le nom de «blockchain».
Chaque bloc est connecté l’un à l’autre via un pointeur de hachage, qui est le hachage des données à l’intérieur du bloc précédent avec l’adresse du bloc précédent. En liant des blocs de données dans ce format, chaque hachage résultant du bloc précédent représente l’état entier de la blockchain puisque toutes les données hachées des blocs précédents sont hachées en un seul hachage.
Ceci est représenté (dans le cas de l’algorithme SHA-256) par une sortie (hachage) comme celle-ci.
b09a57d476ea01c7f91756adff1d560e579057ac99a28d3f30e259b30ecc9dc7
Le hachage ci-dessus est l’empreinte digitale de l’état entier de la blockchain avant elle. L’état de la blockchain avant le nouveau bloc (en tant que données hachées) est l’entrée, et le hachage résultant est la sortie.
Bien qu’il soit possible d’utiliser des hachages cryptographiques sans arbres Merkle, il est extrêmement inefficace et non évolutif. L’utilisation de hachages pour stocker des données dans un bloc dans un format de série prend du temps et est fastidieuse.
Comme vous le verrez, les arbres Merkle permettent une résolution triviale de l’intégrité des données ainsi que le mappage de ces données à travers l’arbre entier à l’aide de preuves Merkle..
Arbres Merkle et preuves Merkle
Nommé d’après Ralph Merkle, qui a breveté le concept en 1979, les arbres Merkle sont fondamentalement des arbres de structure de données où chaque nœud non-feuille est un hachage de ses nœuds enfants respectifs.
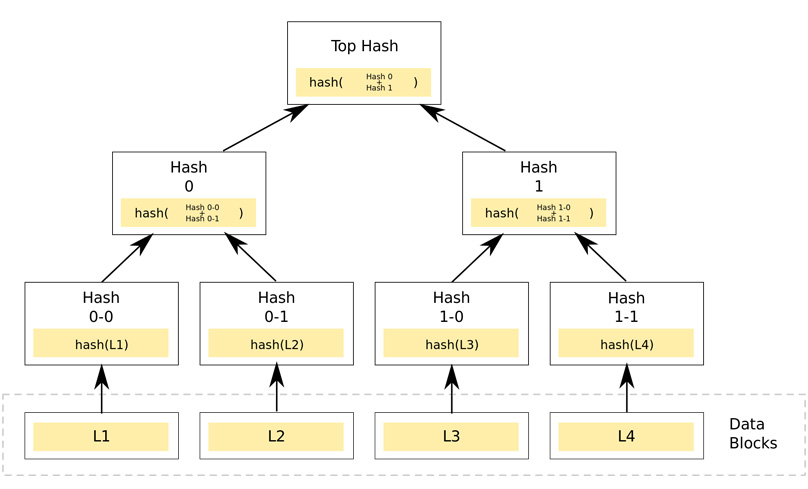
Les nœuds feuilles sont le niveau le plus bas de nœuds de l’arborescence. Au début, cela peut sembler difficile à comprendre, mais si vous regardez la figure couramment utilisée ci-dessous, cela deviendra beaucoup plus facile à comprendre..
Un exemple d’arbre de hachage binaire, Image de Wikipédia
Surtout, remarquez comment les nœuds non-feuilles ou «branches» (représentés par Hash 0-0 et Hash 0-1) sur le côté gauche, sont des hachages de leurs enfants respectifs L1 et L2. De plus, notez comment la branche Hash 0 est le hachage de ses enfants concaténés, les branches Hash 0-0 et Hash 0-1.
L’exemple ci-dessus est la forme la plus courante et la plus simple d’un arbre Merkle connu sous le nom d’arbre Merkle binaire. Comme vous pouvez le voir, il existe un hachage supérieur qui est le hachage de l’arbre entier, connu sous le nom de hachage racine. Essentiellement, les arbres Merkle sont une structure de données qui peut prendre «n» nombre de hachages et le représenter avec un seul hachage.
La structure de l’arborescence permet un mappage efficace de grandes quantités de données arbitrairement grandes et permet une identification facile de l’endroit où se produisent des changements dans ces données. Ce concept permet des preuves Merkle, avec lesquelles quelqu’un peut vérifier que le hachage des données est cohérent tout au long de l’arbre et dans la bonne position sans avoir à regarder l’ensemble des hachages..
Au lieu de cela, ils peuvent vérifier qu’un bloc de données est cohérent avec le hachage racine en ne vérifiant qu’un petit sous-ensemble des hachages plutôt que l’ensemble de données..
Tant que le hachage racine est connu et approuvé publiquement, il est possible pour quiconque souhaite effectuer une recherche de valeur-clé sur une base de données d’utiliser une preuve Merkle pour vérifier la position et l’intégrité d’un élément de données dans une base de données qui a une racine particulière.
Lorsque le hachage racine est disponible, l’arborescence de hachage peut être reçue de n’importe quelle source non fiable et une branche de l’arborescence peut être téléchargée à la fois avec une vérification immédiate de l’intégrité des données, même si l’arborescence entière n’est pas encore disponible.
L’un des avantages les plus importants de la structure arborescente Merkle est la possibilité d’authentifier des ensembles de données arbitrairement volumineux grâce à un mécanisme de hachage similaire utilisé pour vérifier des quantités de données beaucoup plus petites..
L’arbre est avantageux pour distribuer de grands ensembles de données en parties plus petites gérables où la barrière pour la vérification de l’intégrité est considérablement réduite malgré la taille globale des données plus grande..
Le hachage racine peut être utilisé comme empreinte digitale pour un ensemble de données entier, y compris une base de données entière ou représentant l’état entier d’une blockchain. Dans les sections suivantes, nous discuterons de la manière dont Bitcoin et d’autres systèmes implémentent les arbres Merkle..
Arbres Merkle en Bitcoin
La fonction de hachage cryptographique utilisée par Bitcoin est l’algorithme SHA-256. Cela signifie «Secure Hashing Algorithm», dont la sortie est d’une longueur fixe de 256 bits. La fonction de base des arbres Merkle dans Bitcoin est de stocker et éventuellement d’élaguer les transactions dans chaque bloc.
Comme mentionné précédemment, les blocs d’une blockchain sont connectés via des hachages du bloc précédent. Dans Bitcoin, chaque bloc contient toutes les transactions de ce bloc ainsi que l’en-tête du bloc qui se compose de:
- Numéro de version du bloc
- Hash de bloc précédent
- Horodatage
- Objectif de difficulté minière
- Nonce
- Hash de racine de merkle
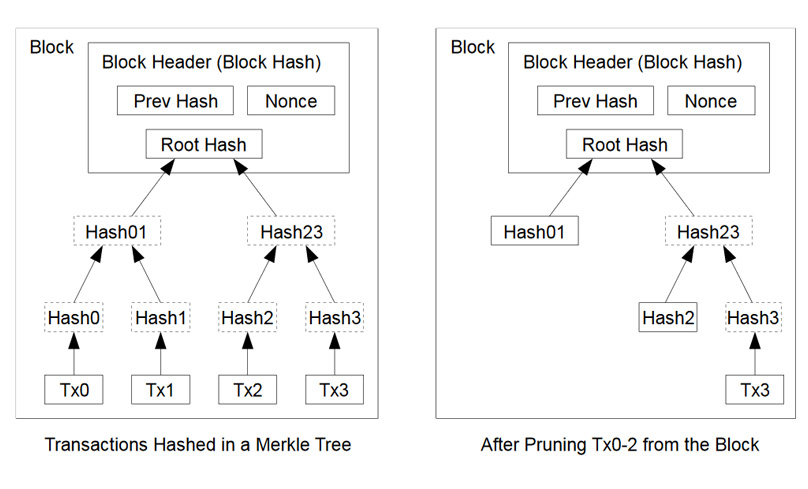
L’image ci-dessous provient du Bitcoin papier blanc et illustre comment l’arbre Merkle s’intègre dans chaque bloc.
Les transactions sont incluses dans des blocs par les mineurs et sont hachées dans le cadre d’un arbre Merkle, conduisant à la racine Merkle qui est stockée dans l’en-tête de bloc. Cette conception présente un certain nombre d’avantages distincts.
Plus particulièrement, comme indiqué dans le livre blanc, cela permet l’existence de nœuds de vérification de paiement simple (SPV), également appelés «clients légers». Ces nœuds n’ont pas besoin de télécharger l’intégralité de la blockchain Bitcoin, seulement les en-têtes de bloc de la plus longue chaîne.
Les nœuds SPV peuvent y parvenir en interrogeant leurs nœuds homologues jusqu’à ce qu’ils soient convaincus que les en-têtes de bloc stockés sur lesquels ils opèrent font partie de la chaîne la plus longue. Un nœud SPV peut ensuite déterminer le statut d’une transaction en utilisant la preuve Merkle pour mapper la transaction à un arbre Merkle spécifique avec le hachage racine de cet arbre Merkle respectif dans un en-tête de bloc qui fait partie de la plus longue chaîne.
De plus, la mise en œuvre par Bitcoin des arbres Merkle permet d’élaguer la blockchain afin d’économiser de l’espace. Ceci est le résultat du seul stockage du hachage racine dans l’en-tête du bloc, par conséquent, les anciens blocs peuvent être élagués en supprimant les branches inutiles de l’arborescence Merkle tout en ne conservant que celles nécessaires à la preuve Merkle.
Implémentation d’arbres Merkle dans d’autres blockchains et systèmes
Bien que Bitcoin ait été la première blockchain à implémenter des arbres Merkle, de nombreuses autres blockchains implémentent des structures d’arbres Merkle similaires ou des versions encore plus complexes..
De plus, l’implémentation de l’arbre Merkle n’est pas seulement limitée aux blockchains et est appliquée à une variété d’autres systèmes.
Ethereum, étant l’autre crypto-monnaie la plus reconnaissable, est également un excellent exemple d’une implémentation différente de l’arbre Merkle. Étant donné qu’Ethereum est complet en tant que plate-forme pour créer des applications beaucoup plus complexes, il utilise une version plus complexe de l’arbre Merkle appelée Merkle Patricia Tree qui est en fait 3 arbres Merkle distincts utilisés pour trois types d’objets. Vous pouvez en savoir plus sur ces arbres Ici.
Enfin, les arborescences Merkle sont des composants importants des systèmes de contrôle de version distribués tels que Git et IPFS. Leur capacité à assurer et vérifier facilement l’intégrité des données partagées entre les ordinateurs dans un format P2P les rend inestimables pour ces systèmes.
Conclusion
Les arbres Merkle font partie intégrante des blockchains et leur permettent efficacement de fonctionner avec une immuabilité et une intégrité des transactions prouvables.
Comprendre le rôle qu’ils jouent dans les réseaux distribués et leur technologie sous-jacente des fonctions de hachage cryptographique est essentiel pour comprendre les concepts de base des crypto-monnaies alors qu’ils continuent de se développer en systèmes plus grands et plus complexes..