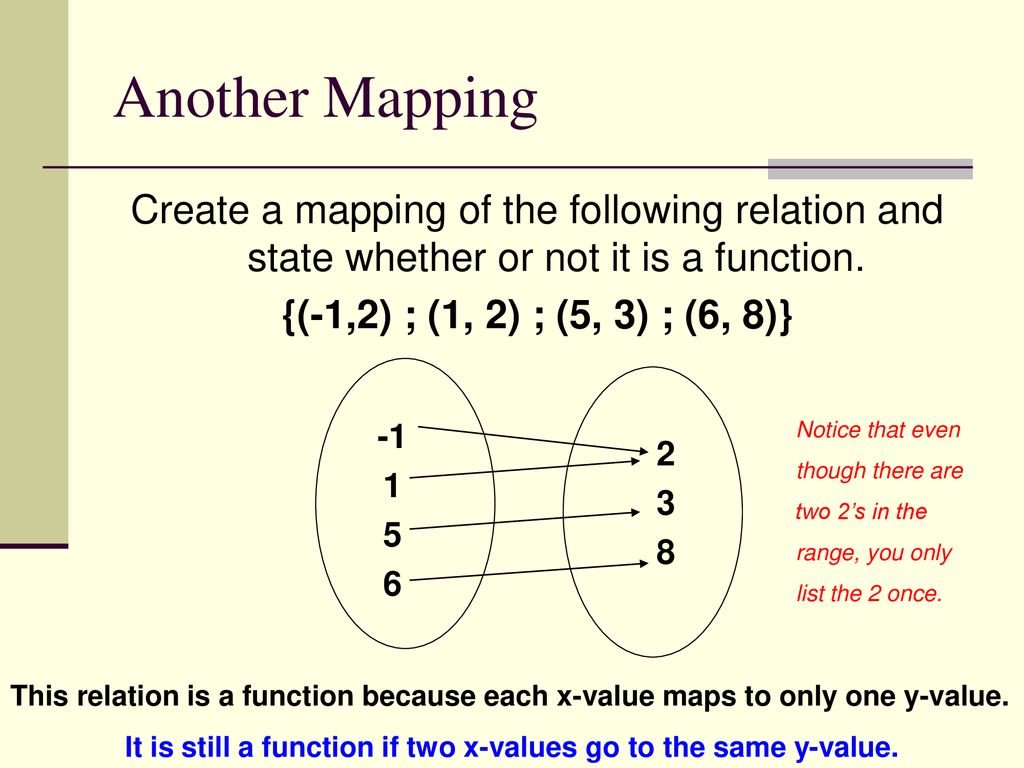
Can a function have multiple same Y-values
To put it concisely: In a function, there can only be one x-value for each y-value. There can be duplicate y-values but not duplicate x-values in a function. When there is one and only one y-value for each x-value (no duplicates in y), it is called a one-to-one function.
Can the range repeat in a function
Repeated values within the domain or range don't have to be listed more than once. In order for a relation to be a function, each x must correspond with only one y value.
What are the Y-values of a function
The variable x is called the independent variable (also sometimes called the argument of the function), and the variable y is called dependent variable (also sometimes called the image of the function.)
What is a function and what is not
This is a non-function. For mapping diagrams. I'm going to use my same definition every x can i have only one y. Value.
Can a function have the same y-intercept
Yes, two different linear functions can have the same y-intercept. To illustrate this, consider the following two linear functions: y = 2x + 5.
Can two different functions have the same variables
Yes, it's ok, every variable has a scope. The scope of a function parameter is that function. So the two int n variables are limited to their respective functions.
Can the range have the same number twice
If there is a number that's there twice or more you only have to write it once. The range is the y number. In a coordinate set, the range would be y which is the second number. Same thing with domain, you only have to write it once of it repeats.
Can the range repeat in a one to one function
One to one function is a special function that maps every element of the range to exactly one element of its domain i.e, the outputs never repeat.
How do you know if Y is a function
You can see this is y squared. We want to solve just for y. So what I'm going to do is I'm going to take the square root of both sides. Remember.
Why is Y =- 2 considered a function
The expression y = 2 is a horizontal line passing through (0, 2). So by vertical line test, y =2 is a function. We can also say that a function assigns a unique output value to each input value.
How do I know if it’s a function
If I put another point right here for example. What. It means is that for this x-value. For I'm getting a y-value of 1.
What can not be a function
Vertical lines are not functions. The equations y = ± x and x 2 + y 2 = 9 are examples of non-functions because there is at least one -value with two or more -values. The vertical line test is a great way to visualize a violation of the definition of a function.
What happens if the y-intercept is the same
If the y-intercepts are the same, the two equations represent the same line and there are INFINITELY MANY SOLUTIONS.
How many y-intercepts can a function have
Although a function can have many x-intercepts, a function can only have one y-intercept. This is because a function must pass the vertical line test in order for it to be a function; if a vertical line intersects the graph of a relation at more than one point, it is not a function.
Can two functions be the same
We say two functions f and g are equal if they have the same domain and the same codomain, and if for every a in the domain, f(a)=g(a).
Can you have the same variable on both sides
To solve an equation that has the same variable on both sides of it, you need to get the variables together on one side of the equation, and then get the numbers together on the other side of the equation.
Can the domain have the same range
Can a function's domain and range be the same Yes. For example, the domain and range of the cube root function are both the set of all real numbers.
What is not true about function
– Function is composed of two quantities: This is not true. A function is a set of ordered pairs, where the first element of each pair is an input and the second element is the corresponding output. Therefore, the statement that is not true about function is "One-to-many correspondence is a function."
Can a function repeat itself
A function that repeats itself after a fixed period ( regular intervals) is called a periodic function. They behave cyclically over a specific time interval.
What makes an equation not a function
Step 1: Solve the equation for , if needed. Step 2: Determine how many outputs, , there are for any input, . A function will only have one or zero outputs for any input. If there is more than one output for a particular input, the equation does not define a function.
Why y2 is not a function
It is not, because the definition of a function includes the requirement that no x will have more than one corresponding y. The parabola you named has its vertex at (0,0) and opens to the right, so every x value > 0 will have two corresponding y values, one positive and one negative.
Is y 2 a constant function
Example: The function y(x) = 2 or just y = 2 is the specific constant function where the output value is c = 2. The domain of this function is the set of all real numbers R. The codomain of this function is just {2}.
How do you tell if it’s a function or not from an equation
Now the next thing i need to do is i'm going to take the square. Root. That is going to get rid of my y or y squared therefore i'm left with y equals. Plus or minus the square root of 4 minus x.
What is the easiest way to identify a function
So this one is a function. So we're gonna say yes it is a function. If you happen to draw a vertical line on your graph.
When can a function not exist
However, if the function cannot be defined, it also does not exist. To summarize when a limit does not exist: A right-hand limit does not exist if f(x) increases or decreases infinitely as the value of x approaches the value of c from the right.