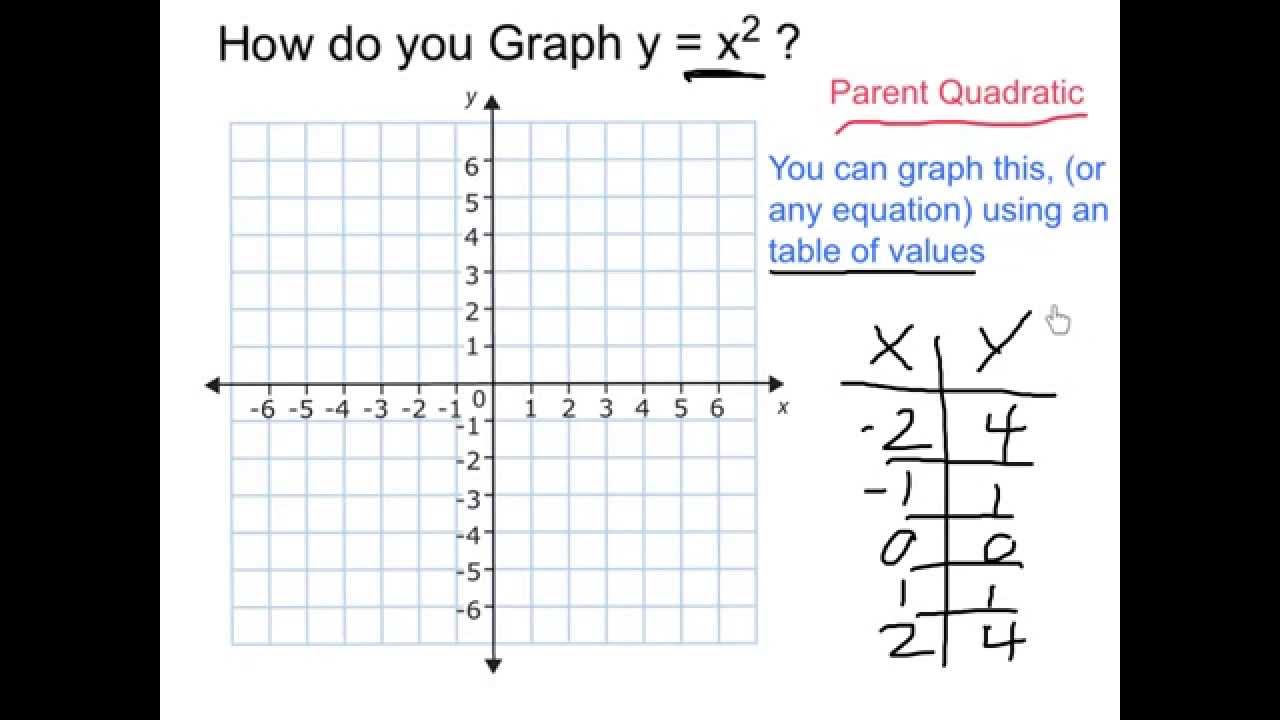
Is Y x2 linear or nonlinear
nonlinear
The equation for the table of values is y = x2. This graph is nonlinear because it forms a curved line and is a parabola, not a straight line.
Does Y x2 represent a linear function
No, the linear equations have a degree of while y = x 2 has the degree of 2, so it is a quadratic equation, not a linear function.
How tell if an equation is linear
So i'm good with there. But can i rewrite it like this and the answer is yes. If you were to kind of look at this. And divide your 5 into x you'd have x over 5 plus 12 over 5..
Which equation is linear
A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0.
Which equation are not linear
An equation is considered “non-linear” when it is not graphed using straight lines. Some examples include $y = 3{x^2} + 1,y = 2{x^3} – 3,y = {x^5} + 43$.
What equation is linear or nonlinear
Linear equations are equations that can be written in the form y = mx + b, where m is the slope and b is the y-intercept. Nonlinear equations are equations that are not in the form y = mx + b.
What if a function is linear
A linear function is a function that represents a straight line on the coordinate plane. For example, y = 3x – 2 represents a straight line on a coordinate plane and hence it represents a linear function. Since y can be replaced with f(x), this function can be written as f(x) = 3x – 2.
Is y x2 a quadratic function
y = x2 is a quadratic equation. It's equivalent to y – x2 = 0, and y – x2 is a quadratic polynomial. xy = 1 is a quadratic equation. It's equivalent to the quadratic equation xy – 1 = 0.
Which is not a linear equation
An equation in which the maximum degree of a term is 2 or more than two is called a nonlinear equation. For example \[3x^{2}\] + 2x + 1 = 0, 3x + 4y = 5, this is the example of nonlinear equations, because equation 1 has the highest degree of 2 and the second equation has variables x and y.
What are 4 examples of linear equation
If the linear equation has two variables, then it is called linear equations in two variables and so on. Some of the examples of linear equations are 2x – 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, 3x – y + z = 3.
Which equations are not linear
A Nonlinear equation can be defined as the equation having the maximum degree 2 or more than 2. A linear equation forms a straight line on the graph. A nonlinear equation forms a curve on the graph. Where x and y are the variables, m is the slope of the line and c is a constant value.
How do you know if a function is linear or not linear
The change in X because when you think about the slope slope is like the rise over the run or the change in Y over change in X if it's linear it's gonna go up at a constant rate meaning that that
What is not a linear function
Algebraically, linear functions are polynomials with highest exponent equal to 1 or of the form y = c where c is constant. Nonlinear functions are all other functions. An example of a nonlinear function is y = x^2. This is nonlinear because, although it is a polynomial, its highest exponent is 2, not 1.
What makes a function linear or not linear
Linear functions have a constant slope for any two points on the line, whereas the slope of nonlinear functions is not constant. The rate of change for linear functions is always constant whereas, for nonlinear functions, it is variable.
How do you prove a function is linear
A linear function must satisfy f(cx)=cf(x) for any number c. The other requirement for a linear function is that applying f to the sum of two inputs x and y is the same thing as adding the results from being applied to the inputs individually, i.e., f(x+y)=f(x)+f(y).
Is a quadratic equation a linear function
Quadratic equations are different than the linear equations in the following ways: A linear equation produces a straight line when we graph it whereas when we graph a quadratic equation we produce a parabola. The slope of a quadratic polynomial unlike the slope of a linear polynomial, is constantly changing.
Why is x2 called a quadratic
This is the case because quadratum is the Latin word for square, and since the area of a square of side length is given by , a polynomial equation having exponent two is known as a quadratic ("square-like") equation. By extension, a quadratic surface is a second-order algebraic surface.
What is an example of not linear
An example of a nonlinear function is y = x^2. This is nonlinear because, although it is a polynomial, its highest exponent is 2, not 1.
What is a nonlinear equation
A Nonlinear equation can be defined as the equation having the maximum degree 2 or more than 2. A linear equation forms a straight line on the graph. A nonlinear equation forms a curve on the graph. The general form of linear equation is, y = mx +c.
What are the 3 linear equations
There are three major forms of linear equations: point-slope form, standard form, and slope-intercept form.
Which function is not linear
A linear function is of the form f(x) = ax + b. Since a nonlinear function is a function that is not a linear, its equation can be anything that is NOT of the form f(x) = ax+b. Some examples of nonlinear functions are: f(x) = x2 is nonlinear as it is a quadratic function.
Is it linear or nonlinear equation
A linear equation has a maximum of one degree. This means you can only raise a variable in the equation to the power of 1. A nonlinear equation has two or more degrees. This means you can only raise a variable in the equation to the power of 2 or higher.
How can you tell if an equation is non linear
It. Might look like that. Doesn't matter what they are they can be graphed in a line a nonlinear equation so this is a parabola it's not a line. This is also not a line.
How do you tell if a function is linear or nonlinear
To see if a table of values represents a linear function, check to see if there's a constant rate of change. If there is, you're looking at a linear function!
How do you tell if a function is linear or nonlinear from an equation
Note: To determine if an equation is a linear function, it must have the form $y = mx + b$ (in which m is the slope and b is the y-intercept). A nonlinear function will not match this form. In a linear equation, the variables appear in first degree only and terms containing products of variables are absent.