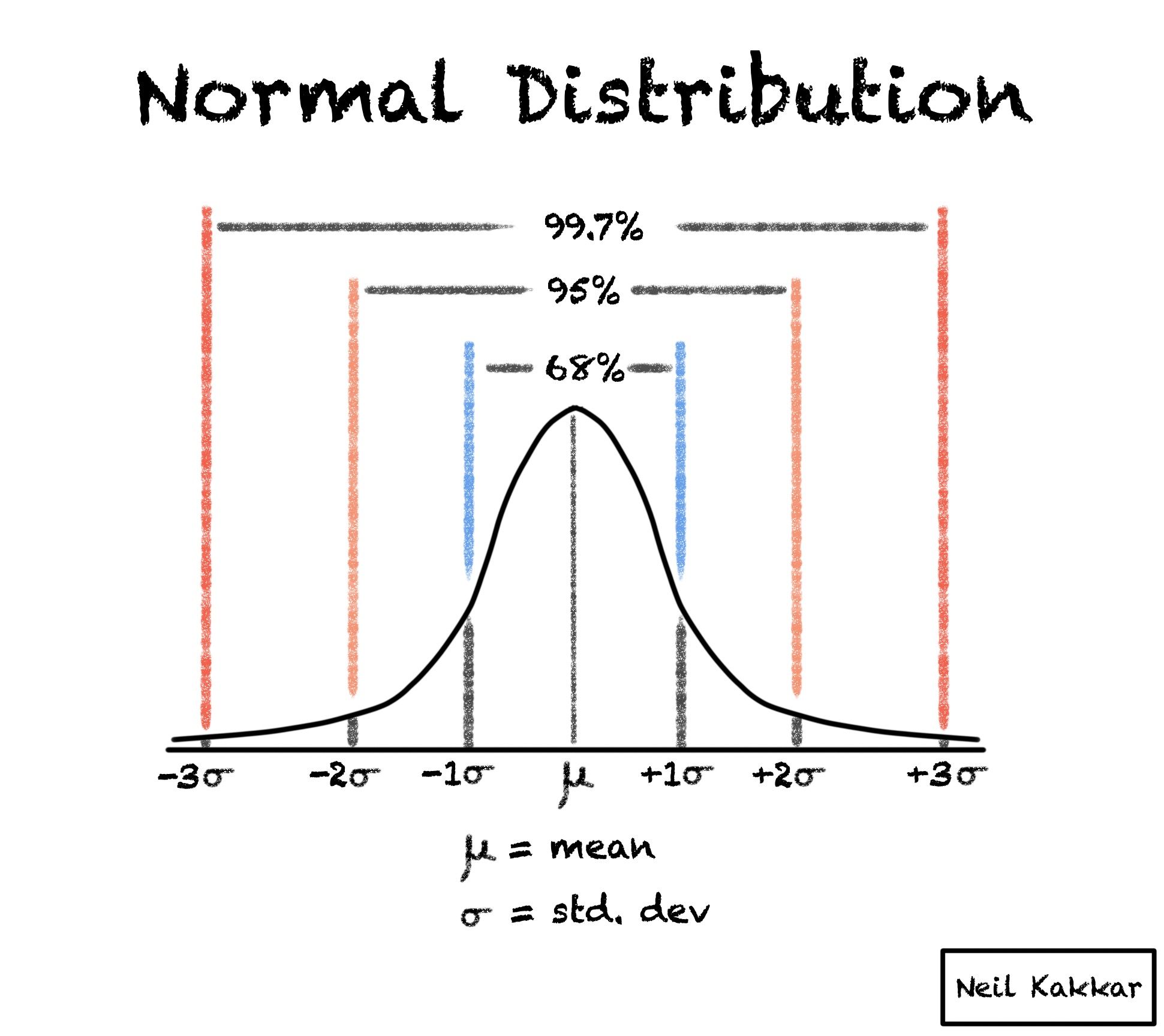
What is the 68 95 and 99.7 rule
In statistics, the 68–95–99.7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie within an interval estimate in a normal distribution: 68%, 95%, and 99.7% of the values lie within one, two, and three standard deviations of the mean, respectively.
What is the 65 98 99 rule
Sixty-eight percent of the data is within one standard deviation (σ) of the mean (μ), 95 percent of the data is within two standard deviations (σ) of the mean (μ), and 99.7 percent of the data is within three standard deviations (σ) of the mean (μ).
What is another name for the 68-95-99.7 rule
These facts are the 68 95 99.7 rule. It is sometimes called the Empirical Rule because the rule originally came from observations (empirical means “based on observation”). The Normal/Gaussian distribution is the most common type of data distribution.
What percentile is 2 sigma
about 95 percent
One standard deviation, or one sigma, plotted above or below the average value on that normal distribution curve, would define a region that includes 68 percent of all the data points. Two sigmas above or below would include about 95 percent of the data, and three sigmas would include 99.7 percent.
What is the 68 92 99.7 rule
The 68-95-99.7 Rule
In the Normal distribution with mean µ and standard deviation σ: Approximately 68% of the observations fall within σ of µ. Approximately 95% of the observations fall within 2σ of µ. Approximately 99.7% of the observations fall within 3σ of µ.
How do you calculate z-score
The formula for calculating a z-score is z = (x-μ)/σ, where x is the raw score, μ is the population mean, and σ is the population standard deviation. As the formula shows, the z-score is simply the raw score minus the population mean, divided by the population standard deviation.
What is the 68-95-99.7 rule for normal distributions explain how it can be used to answer questions about frequencies of data values in a normal distribution
The empirical rule, or the 68-95-99.7 rule, tells you where most of the values lie in a normal distribution: Around 68% of values are within 1 standard deviation of the mean. Around 95% of values are within 2 standard deviations of the mean. Around 99.7% of values are within 3 standard deviations of the mean.
Who created the 68-95-99.7 rule
The 68–95–99.7 was first coined and discovered by Abraham de Moivre in 1733 through his experimentation of flipping 100 fair coins. It was more than 75 years before the normal distribution model was introduced.
Who discovered the 68-95-99.7 rule
Abraham de Moivre
The 68–95–99.7 was first discovered and named by Abraham de Moivre in 1733 during his experimentation of flipping 100 fair coins. This term was coined 75 years before the normal distribution model even was introduced.
What percentile is 1 z-score
Likewise, a Z-score of -1 which is one standard deviation below the mean would be expressed as the 16th percentile.
Is 84th percentile good
In a school setting, students who score near the top of the “Average” range (up to the 84th percentile) are generally considered average, usually meaning that they don't qualify as talented and gifted (TAG).
What is a good z-score
According to the Percentile to Z-Score Calculator, the z-score that corresponds to the 80th percentile is 0.8416. Thus, any student who receives a z-score greater than or equal to 0.8416 would be considered a “good” z-score.
What is the z-score of 2
A z-score equal to 0 represents an element equal to the mean. A z-score equal to 1 represents an element, which is 1 standard deviation greater than the mean; a z-score equal to 2 signifies 2 standard deviations greater than the mean; etc.
What is the difference between the normal distribution and the standard normal distribution
All normal distributions, like the standard normal distribution, are unimodal and symmetrically distributed with a bell-shaped curve. However, a normal distribution can take on any value as its mean and standard deviation. In the standard normal distribution, the mean and standard deviation are always fixed.
Does the 68 95 99.7 rule applies only to skewed or almost skewed distributions
No, the rule is specific to normal distributions and need not apply to any non-normal distribution, skewed or otherwise. Consider for example the uniform distribution on [0,1].
How much is 3 sigma
99.73%
The 3 sigma percentage of accuracy is 99.73% and is used to measure the predictability of outcomes for a desired process.
What is the percentage of 5 sigma
For other results, like the Higgs boson discovery, a five-sigma significance is the 0.00003% likelihood of a statistical fluctuation, as scientists look for data that exceeds the five-sigma value on one half of the normal distribution graph.
What is the 3 sigma level
Three Sigma is the third Sigma level, which dictates that there can only be a margin of error up to three standard deviations from the mean. This means that 99.7% of all outcomes fall within this range of accuracy. All Sigma levels measure the maximum number of allowable defects per one million parts.
What is the z-score of 3
Z score tables sometimes only go up to 3. But depending on the spread of the population, z scores could go on for a while. A Z score of 3 refers to 3 standard deviations. That would mean that more than 99% of the population was covered by the z score.
What percentile is an IQ of 135
99
Summary IQ percentile and rarity
| IQ | Percentile | Top % |
|---|---|---|
| 125 | 95.2 | 4.8 |
| 130 | 97.7 | 2.3 |
| 135 | 99 | 1 |
| 140 | 99.6 | 0.4 |
Is 99% percentile good or bad
What is 99th percentile The 99th percentile is the highest percentile you can get. It means that you are one of the top scorers since you scored higher than 99% of students who took the test. Only 1 in 100 students score in this range, so it places you at the very top of the applicant pool, in terms of SAT scores.
What is a rare z-score
As a rule, z-scores above 2.0 (or below –2.0) are considered “unusual” values. According to the 68-95-99.7 Rule, in a normal population such scores would occur less than 5% of the time. Z-scores between -2.0 and 2.0 are considered “ordinary” values and these represent 95% of the values.
What z-score is too high
A positive z-score says the data point is above average. A negative z-score says the data point is below average. A z-score close to 0 says the data point is close to average. A data point can be considered unusual if its z-score is above 3 or below −3 .
What if the z-score is 1
A Z-score of 1.0 would indicate a value that is one standard deviation from the mean. Z-scores may be positive or negative, with a positive value indicating the score is above the mean and a negative score indicating it is below the mean.
What does a +1 z-score mean
A score of 1 indicates that the data are one standard deviation from the mean, while a Z-score of -1 places the data one standard deviation below the mean. The higher the Z-score, the further from the norm the data can be considered to be.