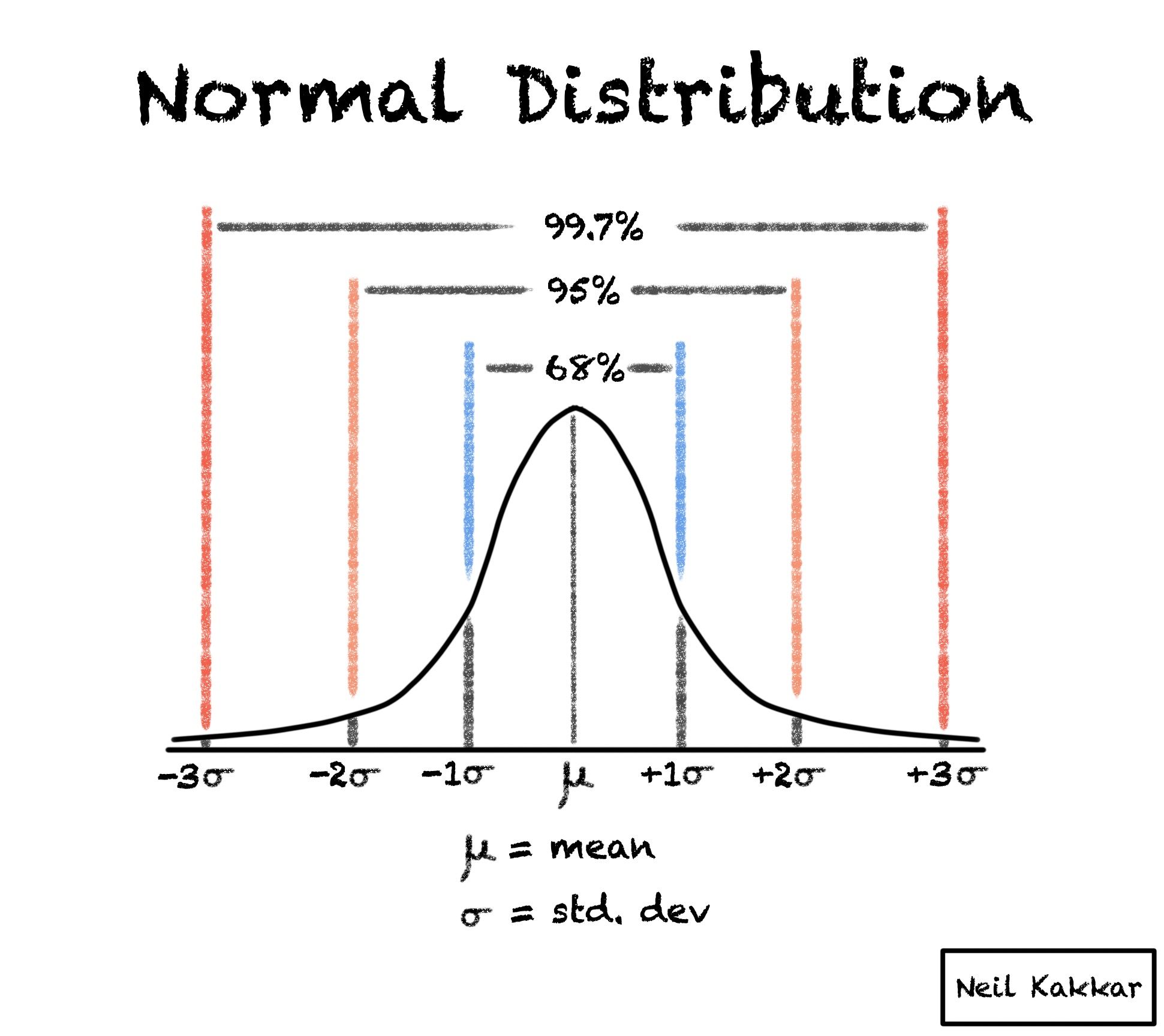
What is the 68-95-99.7 rule used for
In statistics, the 68–95–99.7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie within an interval estimate in a normal distribution: 68%, 95%, and 99.7% of the values lie within one, two, and three standard deviations of the mean, respectively.
What is the 68 92 99.7 rule
The 68-95-99.7 Rule
In the Normal distribution with mean µ and standard deviation σ: Approximately 68% of the observations fall within σ of µ. Approximately 95% of the observations fall within 2σ of µ. Approximately 99.7% of the observations fall within 3σ of µ.
What is the 68-95-99.7 rule bell curve
Sixty-eight percent of the data is within one standard deviation (σ) of the mean (μ), 95 percent of the data is within two standard deviations (σ) of the mean (μ), and 99.7 percent of the data is within three standard deviations (σ) of the mean (μ).
What is the 68-95-99.7 rule about what of values are within one standard deviation of the mean
Approximately 68%
Empirical Rule or 68-95-99.7% Rule
Approximately 68% of the data fall within one standard deviation of the mean. Approximately 95% of the data fall within two standard deviations of the mean. Approximately 99.7% of the data fall within three standard deviations of the mean.
How do you use the 68 95 and 99.7 rule examples
And half of this is 34%. Giving us our area from zero to one. The next half goes from zero to negative two. But we know that within two standard deviations. From the mean we have an area of 95%.
What is 1 sigma 2 sigma 3 sigma
One standard deviation, or one sigma, plotted above or below the average value on that normal distribution curve, would define a region that includes 68 percent of all the data points. Two sigmas above or below would include about 95 percent of the data, and three sigmas would include 99.7 percent.
Who created the 68 95 99.7 rule
The 68–95–99.7 was first coined and discovered by Abraham de Moivre in 1733 through his experimentation of flipping 100 fair coins. It was more than 75 years before the normal distribution model was introduced.
What is the 68 95 99.7 rule quizlet
Approximately 68% of the observations are within 1 standard deviation of the mean. Approximately 95% of the observations are within 2 standard deviations of the mean. Approximately 99.7% of the observations are within 3 standard deviations of the mean.
Do all normal curves satisfy the 68-95-99.7 rule
Remember that the rule applies to all normal distributions.
What is the 95 rule with mean and standard deviation
The 95% Rule states that approximately 95% of observations fall within two standard deviations of the mean on a normal distribution. The normal curve showing the empirical rule.
Does the 68-95-99.7 rule applies only to skewed or almost skewed distributions
No, the rule is specific to normal distributions and need not apply to any non-normal distribution, skewed or otherwise. Consider for example the uniform distribution on [0,1].
How much is 3 sigma
99.73%
The 3 sigma percentage of accuracy is 99.73% and is used to measure the predictability of outcomes for a desired process.
What is 3 sigma and 5 sigma
The higher the “-sigma” value, the less likely it is that a signal is just a random fluctuation in the background model. Remember, in simple terms, a “3-sigma” signal has only a 0.3% chance of being a background fluctuation, and a “5-sigma” signal is has just a 0.00006% chance!
How much is 4 sigma
Four Sigma quality – This level of performance yields a defect-free product 99.349% of the time. With four sigma quality 73 applications would need to be corrected every day. Five Sigma quality – Five Sigma performance produces defect-free products and services 99.977% of the time.
Who created the 68-95-99.7 rule
The 68–95–99.7 was first coined and discovered by Abraham de Moivre in 1733 through his experimentation of flipping 100 fair coins. It was more than 75 years before the normal distribution model was introduced.
Does the 68 95 99.7 rule applies only to skewed or almost skewed distributions
No, the rule is specific to normal distributions and need not apply to any non-normal distribution, skewed or otherwise. Consider for example the uniform distribution on [0,1].
Can I use Z test for skewed data
You can then make assumptions about the proportion of observations below or above specific Z-values. If however, the original distribution is skewed, then the Z-score distribution will also be skewed. In other words converting data to Z-scores does not normalize the distribution of that data!
Is 3-sigma better than 6 Sigma
3 sigma percentage is primarily used for manufacturing processes that allow for a 93.73% level of accuracy, and as a potential foundation for further process improvement. 6 sigma percentage is used for business activities that require the higher, 99.9997% positive outcome.
What percentage is 4.5 sigma
99.99966%
Sigma levels
| Sigma level | Sigma (with 1.5σ shift) | Percentage yield |
|---|---|---|
| 4 | 2.5 | 99.38% |
| 5 | 3.5 | 99.977% |
| 6 | 4.5 | 99.99966% |
| 7 | 5.5 | 99.9999981% |
What is sigma 5 vs sigma 6
5S focuses on eliminating waste and inefficiencies in the workplace. This methodology can be applied to every department and action that takes place. On the other hand, Six Sigma is a process improvement strategy that eliminates defects by implementing standard processes, identifying problem areas, and more.
How rare is 5 sigma
In most cases, a five-sigma result is considered the gold standard for significance, corresponding to about a one-in-a-million chance that the findings are just a result of random variations; six sigma translates to one chance in a half-billion that the result is a random fluke.
Is there a 5 sigma
A result that has a statistical significance of five sigma means the almost certain likelihood that a bump in the data is caused by a new phenomenon, rather than a statistical fluctuation. Scientists calculate this by measuring the signal against the expected fluctuations in the background noise across the whole range.
Can you use z scores if data is not normally distributed
Non-normal distributions can also be transformed into sets of Z-scores. In this case the standard normal table cannot be consulted, since the shape of the distribution of Z-scores is the same as that for the original non-normal distribution.
What is the z-score for skewness and kurtosis
A z-test is applied for normality test using skewness and kurtosis. A z-score could be obtained by dividing the skew values or excess kurtosis by their standard errors.
Is 2 sigma better than 6 Sigma
The more number of standard deviations between process average and acceptable process limits fits, the less likely that the process performs beyond the acceptable process limits, and it causes a defect. This is the reason why a 6σ (Six Sigma) process performs better than 1σ, 2σ, 3σ, 4σ, 5σ processes.