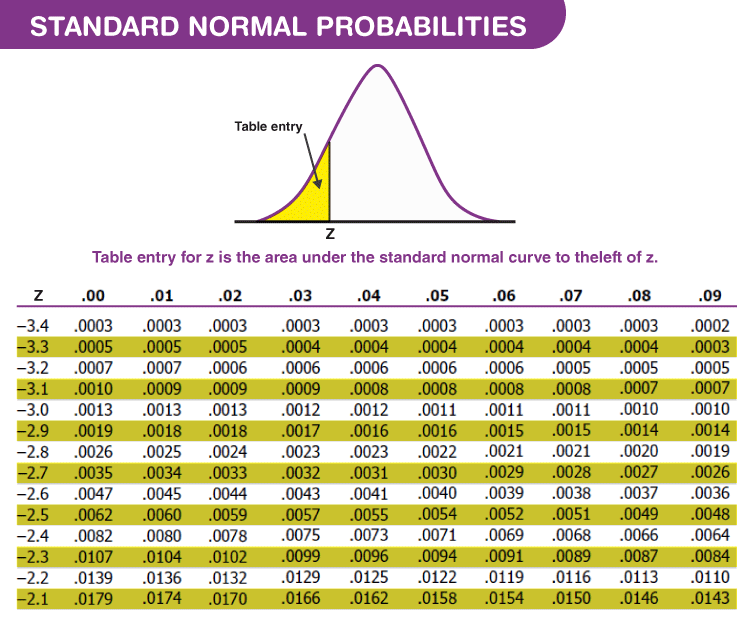
What is the normal Z distribution
The standard normal distribution, also called the z-distribution, is a special normal distribution where the mean is 0 and the standard deviation is 1.
Why is it important to standardize the normal distribution
The normal distribution is an important probability distribution in math and statistics because many continuous data in nature and psychology display this bell-shaped curve when compiled and graphed.
What is an example of a standard normal distribution
What are some real life examples of normal distributions In a normal distribution, half the data will be above the mean and half will be below the mean. Examples of normal distributions include standardized test scores, people's heights, IQ scores, incomes, and shoe size.
What are the properties of the standard normal distribution
What are the properties of normal distributions Normal distributions have key characteristics that are easy to spot in graphs: The mean, median and mode are exactly the same. The distribution is symmetric about the mean—half the values fall below the mean and half above the mean.
What does a z-score of 2.5 mean
2.5 standard deviations
Z-scores are standard deviations. If, for example, a tool returns a z-score of +2.5, you would say that the result is 2.5 standard deviations. Both z-scores and p-values are associated with the standard normal distribution as shown below.
What is 95% normal Z
For the standard normal distribution, P(-1.96 < Z < 1.96) = 0.95, i.e., there is a 95% probability that a standard normal variable, Z, will fall between -1.96 and 1.96.
How do you know if your data is normally distributed
In order to be considered a normal distribution, a data set (when graphed) must follow a bell-shaped symmetrical curve centered around the mean.
How do you calculate normalization z-score
The formula for calculating a z-score is z = (x-μ)/σ, where x is the raw score, μ is the population mean, and σ is the population standard deviation. As the formula shows, the z-score is simply the raw score minus the population mean, divided by the population standard deviation.
Is a normal score the expected z-score of a data value
A normal score is the expected Z-score of the data value if the distribution of the random variable is normal. The expected Z-score of an observed value will depend upon the number of observations in the data set.
What is the z-value to the right of the mean such that 85% of the total area under the standard normal distribution curve lies to the left of
The z-value that has 85% of the total area to the left of it under the standard normal distribution is 1.03643. Locate the p-value in the z-table to obtain . Therefore, the z-value which has that 85% of the total area under the standard normal distribution is 1.03643.
What is the 68 95 99.7 rule
Key Takeaways. The Empirical Rule states that 99.7% of data observed following a normal distribution lies within 3 standard deviations of the mean. Under this rule, 68% of the data falls within one standard deviation, 95% percent within two standard deviations, and 99.7% within three standard deviations from the mean.
What are the properties of Z distribution and T distribution
The Z distribution is a special case of the normal distribution with a mean of 0 and standard deviation of 1. The t-distribution is similar to the Z-distribution, but is sensitive to sample size and is used for small or moderate samples when the population standard deviation is unknown.
What if the z-score is greater than 2
z-score is a measure of how close the given data point is to the mean of the values given with the standard deviation. If the z-score is less than -2 or greater than 2, then the data is unusual. Therefore, a data value is considered unusual if its z-score is less than minus 2 or greater than 2.
What z-score is too high
A positive z-score says the data point is above average. A negative z-score says the data point is below average. A z-score close to 0 says the data point is close to average. A data point can be considered unusual if its z-score is above 3 or below −3 .
What is Z critical for 95%
If you are using the 95% confidence level, for a 2-tailed test you need a z below -1.96 or above 1.96 before you say the difference is significant. For a 1-tailed test, you need a z greater than 1.65. The critical value of z for this test will therefore be 1.65.
What is the z for 90 confidence interval
1.645
Step #5: Find the Z value for the selected confidence interval.
| Confidence Interval | Z |
|---|---|
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
| 99.5% | 2.807 |
How do you know if a distribution is not normal
Non-normal distributions may lack symmetry, may have extreme values, or may have a flatter or steeper “dome” than a typical bell. There is nothing inherently wrong with non-normal data; some traits simply do not follow a bell curve. For example, data about coffee and alcohol consumption are rarely bell shaped.
How do you interpret a normality test
If the Sig. value of the Shapiro-Wilk Test is greater than 0.05, the data is normal. If it is below 0.05, the data significantly deviate from a normal distribution.
What do z-scores tell you
Z-score indicates how much a given value differs from the standard deviation. The Z-score, or standard score, is the number of standard deviations a given data point lies above or below mean. Standard deviation is essentially a reflection of the amount of variability within a given data set.
How do you interpret z-score
Z-scores are measured in standard deviation units.
A Z-score of 2.5 means your observed value is 2.5 standard deviations from the mean and so on. The closer your Z-score is to zero, the closer your value is to the mean. The further away your Z-score is from zero, the further away your value is from the mean.
What is the z-value for normal distribution 95%
-1.96
The critical z-score values when using a 95 percent confidence level are -1.96 and +1.96 standard deviations. The uncorrected p-value associated with a 95 percent confidence level is 0.05.
What is the appropriate value of Z to use in an 80% confidence interval
1.282
Step #5: Find the Z value for the selected confidence interval.
| Confidence Interval | Z |
|---|---|
| 80% | 1.282 |
| 85% | 1.440 |
| 90% | 1.645 |
| 95% | 1.960 |
What proportion of people are expected to have IQ scores between 85 and 115
68% of people have IQs between 85 and 115 (100 +/- 15). 95% have IQs between 70 and 130 (100 +/- (2*15).
Do all normal curves satisfy the 68-95-99.7 rule
Remember that the rule applies to all normal distributions.
How do you choose a T or Z distribution
How to Determine When to Use a z-Distribution or a t-DistributionIf the population standard deviation is known, use the z-distribution.If the population standard deviation is not known, use the t-distribution.