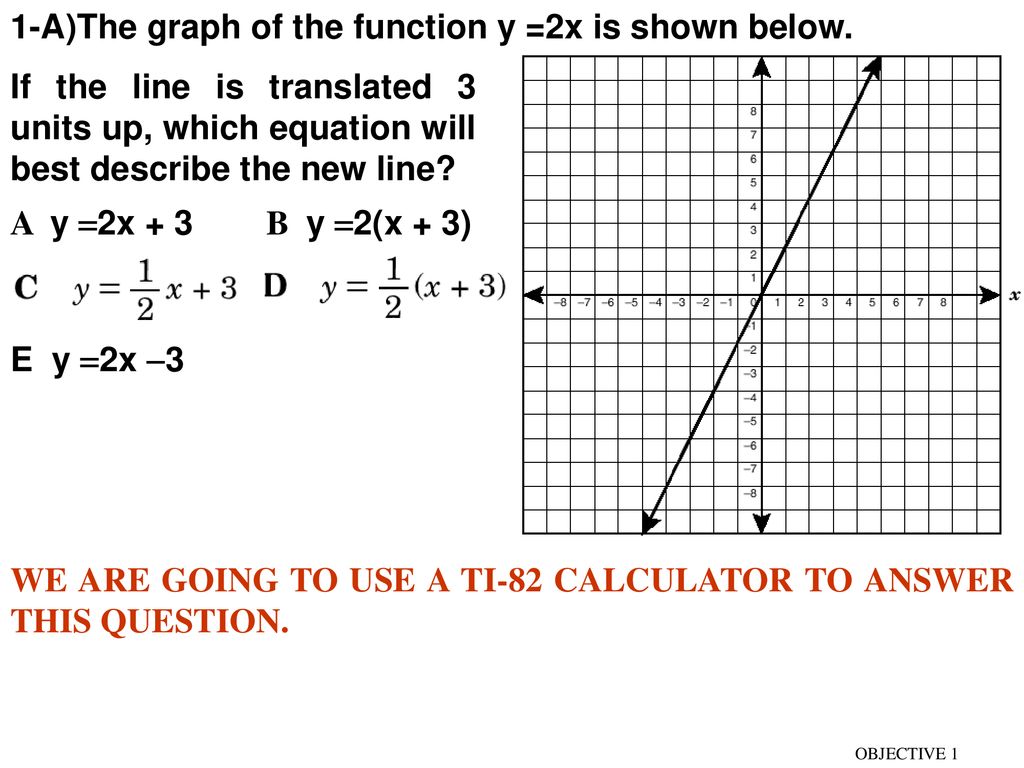
What function is y 2x
So these are the points that we'll graph for the linear equation y equals 2x. So x is zero y is zero. So we find x is zero.
What type of equation is a function
A function is an equation that has only one answer for y for every x. A function assigns exactly one output to each input of a specified type. It is common to name a function either f(x) or g(x) instead of y.
What kind of function is f x )= x2
quadratic function
Graphs of polynomial functions
We have already said that a quadratic function is a polynomial of degree 2. Here are some examples of quadratic functions: f(x) = x2, f(x)=2×2, f(x)=5×2.
Is y x2 a linear function
No, the linear equations have a degree of while y = x 2 has the degree of 2, so it is a quadratic equation, not a linear function.
What is Y =- 2x on a graph
And that's where the line is going to cross through the y-axis. So we have the y-intercept. Is 0 come down here to 0. And that's our first point for m the slope.
Is Y =- x2 a function
Yes it is. Using the definition of a function, y=x^2 is a function because for every x-value in your domain, you will only get 1 unique y-value. A quick check you can do is to use the vertical line test.
What are the 4 different types of functions
Constant Function: The polynomial function of degree zero. Linear Function: The polynomial function of degree one. Quadratic Function: The polynomial function of degree two. Cubic Function: The polynomial function of degree three.
How do you identify if it is a function or not
In these problems we're being asked to determine which of these things are functions. And the basic idea of a function is that you put in some value for X and get out something for Y.
What are types of functions
Types of FunctionsOne-one Function (Injective Function)Many-one Function.Onto Function (Surjective Function)Into Function.Polynomial Function.Linear Function.Identical Function.Quadratic Function.
Is Y =- 5 a horizontal line
y = − 5 is a horizontal line that crosses the -axis at -5. x = − 2 is a vertical line that crosses the -axis at -2.
How is the graph of y =- 2x 2
And then on the y we have minus 2. So go down minus 2.. Then we have 1 on the x. And then 0 on the y. So we'll leave that right there. Finally we have minus 1 on the x. And minus 4 on the y.
What graph represents y =- 2x 3
And over 1 and again. I can go up 2 over 1. I don't have too many points I can do that way but of course it's going to extend in the opposite. Direction up.
How do I know if it’s a function or not a function
Use the vertical line test to determine whether or not a graph represents a function. If a vertical line is moved across the graph and, at any time, touches the graph at only one point, then the graph is a function. If the vertical line touches the graph at more than one point, then the graph is not a function.
Is y x2 an exponential function
If you think of functions with exponents, you're probably used to seeing something like this. That's the graph of y = x2, and it is indeed a function with an exponent. But it's not an exponential function. In an exponential function, the independent variable, or x-value, is the exponent, while the base is a constant.
What are the 8 types of functions
There are actually 8 types of functions. These eight different functions are linear, power, quadratic, polynomial, rational, exponential, logarithmic, and sinusoidal.
What are functions 3 types
Types of Function – Based on Equation
Linear Function: The polynomial function of degree one. Quadratic Function: The polynomial function of degree two. Cubic Function: The polynomial function of degree three.
How do you tell if a function is a function or not on a graph
And different y-coordinates the vertical line goes through two points on the graph. And what that means is that this graph does not represent a function.
How do you prove a function is a function
Notice that to prove a function, f : A → B is one-to-one we must show the following: (∀x ∈ A)(∀y ∈ A)[(x = y) → (f(x) = f(y))]. This is equivalent to showing (∀x ∈ A)(∀y ∈ A)[(f(x) = f(y)) → (x = y)].
What are the 4 of functions
Originally identified by Henri Fayol as five elements, there are now four commonly accepted functions of management that encompass these necessary skills: planning, organizing, leading, and controlling. 1 Consider what each of these functions entails, as well as how each may look in action.
Is Y =- 2 a horizontal line
y = 2 is a horizontal line that crosses the -axis at 2. y = − 2 is a horizontal line that crosses the -axis at -2.
Is Y =- 7 horizontal or vertical
Answer and Explanation:
The graph of y = 7 is a horizontal line.
Is Y =- 2x 2 a function
And then on the y we have minus 2. So go down minus 2.. Then we have 1 on the x. And then 0 on the y. So we'll leave that right there. Finally we have minus 1 on the x. And minus 4 on the y.
How do you graph y =- 2 on a graph
We get another point on the graph. 1 comma negative 2 rise 0 and run 1 get another point. So you can see here. We get the horizontal. Line passing through 0 negative 2.
What does Y =- 2x look like on a graph
And that's where the line is going to cross through the y-axis. So we have the y-intercept. Is 0 come down here to 0. And that's our first point for m the slope.
What type of function is y =- 2x 3
And my y-intercept is going to be 3 start the process of graphing. By graphing the y intercept. By definition the y-intercept is where the equation crosses the y axis. We know that's at 3.