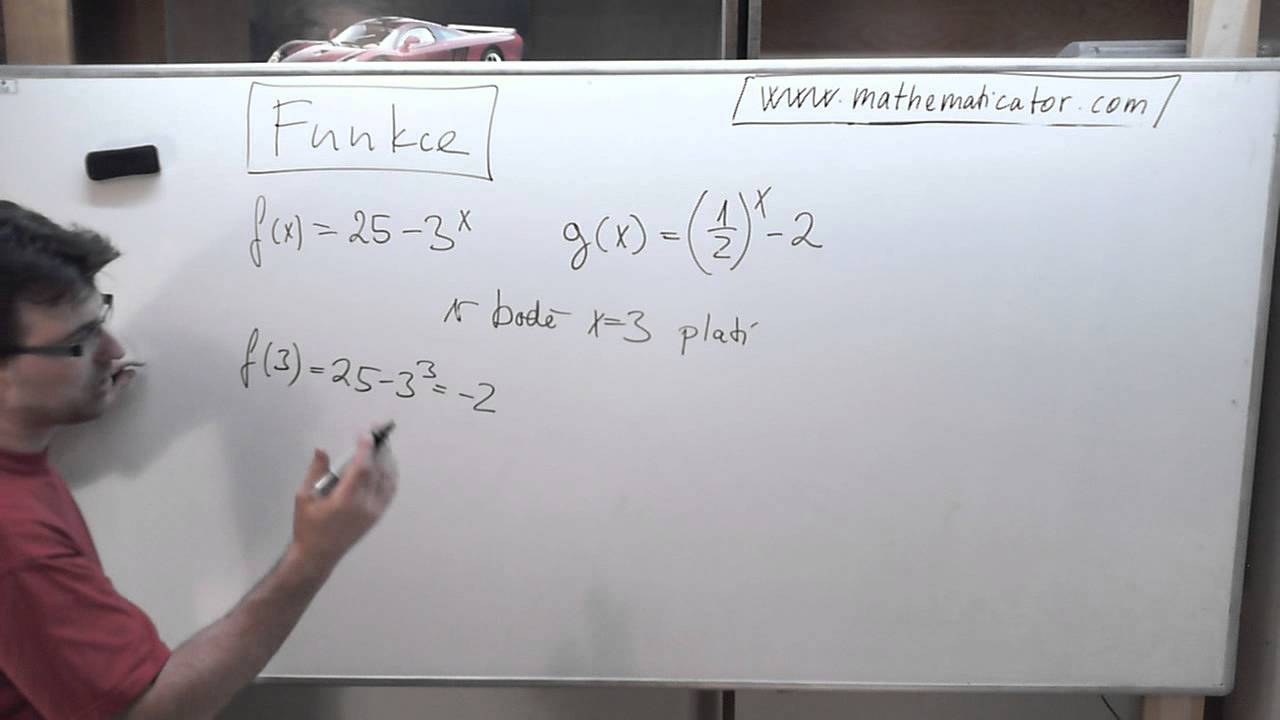Jak se pocita hodnota funkce
Hodnota závisle proměnné je (pro danou funkci) jednoznačně určena hodnotou x – proto 'závisle' proměnná. O funkcích f a g řekneme, že jsou si rovny v případě, že jsou totožné definiční obory D(f)=D(g) a zároveň pro všechna x z definičního oboru jsou si rovny funkční hodnoty f(x)=g(x).
Co je to obor hodnot funkce
Obor hodnot je naopak množina všech reálných čísel y, která dostaneme jako výstupní hodnotu funkce f, jestliže za x dosadíme všechny přípustné hodnoty z D(f). Obor hodnot funkce f značíme H(f).
Co to je argument funkce
To, s čím funkci voláme (to, co dosadíme za x), se nazývá argument funkce. Může se to zdát trochu zmatené, ale pokud máme funkci f(x) a zavoláme ji s hodnotou tři f(3), pak x je parametr funkce a 3 je argument funkce. Argument je ta samotná hodnota, se kterou funkci voláme.
Co je to funkce
Funkce je předpis, který každému číslu x z definičního oboru M přiřadí právě jedno y z oboru hodnot N. Funkci obvykle zapisujeme ve tvaru y = f(x), či ji můžeme vyjádřit explicitně f:y = x kde proměnná x je argument funkce.
Archiv
Kdy to není funkce
U funkce to bude vždycky 1 výstup, 1 prvek z oboru hodnot, který se váže na ten prvek z definičního oboru. Pokud bychom měli jeden prvek z definičního oboru, ten bychom vložili do krabičky, která má být funkcí, a dostali bychom ne 1 prvek z oboru hodnot, ale nějaké y, nějaké z, nějaké e, tak toto není funkce.
Jak se zapisuji funkce
Pravidlo f, které každému prvku množiny A přiřadí jediný prvek množiny B se nazývá funkce (přesněji: reálná funkce jedné reálné proměnné). Zapisujeme f:A→B. Skutečnost, že prvku a∈A je přiřazen prvek b∈B zapisujeme takto: f(a)=b.
Co je d f
Definiční obor funkce je množina všech hodnot (čísel), kterých může proměnná x nabývat. Definiční obor funkce, kterou si pojmenujeme f, budeme značit D(f). Kdybychom si funkci pojmenovali jinak, například brrr, tak její definiční obor budeme značit D(brrr).
Jak otevřít argumenty funkce
Seznam dostupných funkcí zobrazíte kliknutím na buňku a stisknutím SHIFT + F3, který otevře dialogové okno Vložit funkci . 3. argumenty. Argumenty mohou být čísla, text, logické hodnoty pravda nebo NEPRAVDA, matice, chybové hodnoty jako #N/a nebo odkazy na buňky.
Co je to prostá funkce
Jestliže funkce f nabývá pro každé dva různé argumenty různé funkční hodnoty, pak tuto funkci nazýváme prostou.
Jak poznat jestli je to funkce nebo ne
Pokud bychom měli jeden prvek z definičního oboru, ten bychom vložili do krabičky, která má být funkcí, a dostali bychom ne 1 prvek z oboru hodnot, ale nějaké y, nějaké z, nějaké e, tak toto není funkce. U funkce musíme mít pro 1 vstup vždycky 1 výstup.
Co to je prostá funkce
Jestliže je funkce na nějaké množině ryze monotonní, pak tam musí být prostá. To mimo jiné znamená, že jestliže je funkce spojitá na nějakém intervalu I, diferencovatelná na jeho vnitřku, ta derivace není nikde nula a má všude stejné znaménko, pak je tato funkce prostá na I.
Jak určit d f
Nulou neumíme dělit, stejně tak nula nesmí být ve jmenovateli zlomku. Jiné omezení dělení nemá. Proto můžeme za x dosadit jakékoliv reálné číslo kromě nuly. Definiční obor je tak roven: D(f) = ℝ ∖ {0}.
Co je to Arcsin
Arcsin, neboli arcus sinus je inverzní funkce k funkci sinus. Její argument musí být z intervalu -1 až 1 včetně.
Jak použít funkcí IF
Funkce KDYŽ, jedna z logických funkcí, vrátí jednu hodnotu, pokud se zadaná podmínka vyhodnotí jako Pravda, a jinou hodnotu, pokud se vyhodnotí jako Nepravda. Příklady: =KDYŽ(A2>B2;"Překročil se rozpočet.";"OK")
Jak použít funkcí Sumif
Vzorec =SUMIF(B2:B5;"Jan";C2:C5) například vypočítá součet pouze těch hodnot v oblasti C2:C5, u kterých mají odpovídající buňky v oblasti B2:B5 hodnotu Jan. Pokud chcete sečíst buňky na základě více kritérií, přečtěte si článek Funkce SUMIFS.
Jak se pozna prostá funkce
Jestliže funkce f nabývá pro každé dva různé argumenty různé funkční hodnoty, pak tuto funkci nazýváme prostou.
Co je Arctan
Vrátí arkustangens (inverzní funkce k funkci tangens) zadaného čísla. Arkustangens je úhel, jehož tangens je zadané číslo. Výsledný úhel je udáván v radiánech v intervalu -pí/2 až pí/2.
Kdy je síň 0
Sinus a kvadranty
| Stupně | Radiány | sin (x) |
|---|---|---|
| 0° | 0 | 0 |
| 90° | π/2 | 1 |
| 180° | π | 0 |
| 270° | 3π/2 | −1 |
Jak vložit funkcí když do funkce Když
Pokud jste klikli na KDYŽ, zobrazí se v dialogovém okně Argumenty funkce argumenty funkce KDYŽ. Pokud chcete vnořit jinou funkci, můžete ji zadat do pole argumentu. Můžete třeba zadat SUMA(G2:G5)do Value_if_true funkce KDYŽ. Zadejte všechny další argumenty, které jsou potřeba k dokončení vzorce.
Jak na funkcí Svyhledat
Funkce SVYHLEDAT se používá k vyhledání hodnoty v tabulce. Příklady: =SVYHLEDAT(A2;A10:C20;2;PRAVDA) =SVYHLEDAT("Hernady";B2:E7;2;NEPRAVDA)
Jak sečíst hodnoty v Excelu
Vyberte buňku vedle čísel, která chcete sečíst, na kartě Domů klikněte na Automatické shrnutí, stiskněte Enter a máte hotovo. Když kliknete na Automatickéshrnutí, Excel automaticky zadá vzorec (který používá funkci SUMA)k sečtení čísel.
Jak použít funkcí Countifs
Funkci COUNTIF, jednu ze statistických funkcí, můžete používat ke zjištění počtu buněk, které splňují určité kritérium, třeba ke spočítání, kolikrát se konkrétní město zobrazuje v seznamu zákazníků. Ve své nejjednodušší formě COUNTIF říká: =COUNTIF(Kde chcete hledat, Co chcete hledat)
Jak zadat do kalkulačky Arcsin
Inverzní goniometrické funkce
Před stiskem samotné klávesy sin, cos nebo tan, je třeba stisknout klávesu, která bývá označena symbolem INV, Shift, 2nd, nebo f–1. Inverzní funkce k sin bývá označována sin–1 nebo arcsin.
Jak si zapamatovat hodnoty goniometrických funkcí
hodnoty goniometrických funkcí dosahují jednu z hodnot 0, -1, 1 (jedna z funkcí je nulová, druhá nenulová). Hodnotu sinu i cosinu pro libovolný z těchto úhlů snadno určíme tím, že si představíme koncové rameno úhlu a vybereme ze tří možných hodnot.
Co to je cosinus
V pravoúhlém trojúhelníku bývá definována jako poměr přilehlé odvěsny a přepony. Definici lze konzistentně rozšířit jak na celá reálná čísla, tak i do oboru komplexních čísel. Grafem kosinu v reálném oboru je kosinusoida (posunutá sinusoida).