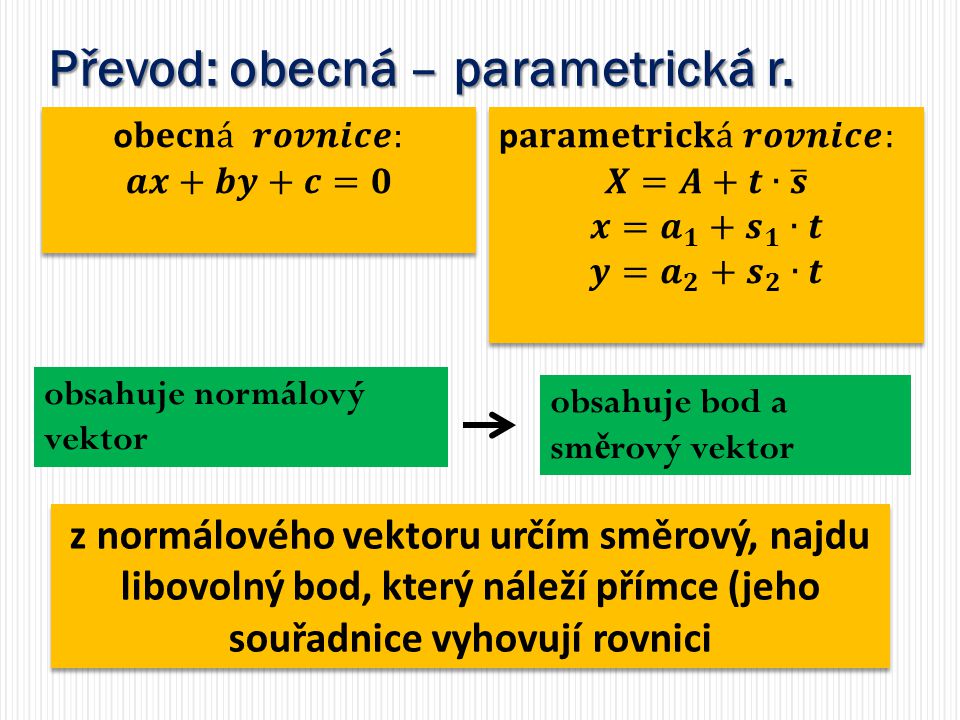
Jak převést obecnou rovnici roviny na parametrickou
K získání parametrického vyjádření roviny potřebujeme znát jeden její bod a dva vektory, které v ní leží, přičemž jeden nesmí být násobkem druhého. Z obecné rovnice sice vyčteme souřadnice normálového vektoru, ale ty v tomto případě nemůžeme nijak využít.
Archiv
Jak udělat z obecně rovnice přímky parametrickou
x=a1+tu1y=a2+tu2 , t∈R . Tyto rovnice nazýváme parametrickými rovnicemi přímky p procházející bodem A se směrovým vektorem →u. Pro různé volby parametru t∈R pak dostáváme souřadnice různých bodů přímky p. Uvědomte si, že směrový vektor →u=(u1,u2) přímky p je určen až na nenulový násobek, tj.
Archiv
Jakou obecnou rovnici má rovina s parametrickým vyjádřením
Potom každý bod X roviny ABC můžeme psát ve tvaru vztahu: X = A + t * u → + s * v → , kde t, s jsou reálná čísla. Tento vztah se nazývá parametrická rovnice roviny (nebo také parametrické vyjádření roviny) ABC.
Archiv
Jak převést směrový vektor na Normálový
Při daném směrovém vektoru nám k získání vektoru normálového stačí prohodit souřadnice a u jedné z nich změnit znaménko.
Archiv
Jak zjistit jestli bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Co to je rovina
Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Jinak řečeno jde o dvoudimenzionální afinní prostor.
Co platí pro dva obecně kolmé vektory
3) dva vektory a , b jsou na sebe kolmé právě tehdy, když jejich skalární součin je roven nule. Vektorový součin je další operace s vektory. Už víme, že výsledek skalárního součinu dvou vektorů je číslo, výsledkem vektorového součinu je vektor.
Jak Vypocitat parametrickou rovnici
Každou přímku lze zapsat nějakým parametrickým vyjádřením a každé parametrické vyjádření popisuje nějakou přímku. Když parametrickou rovnici přímky p(A, u), kde A[a1; a2] a u = (u1; u2), zapíšeme pomocí souřadnic, získáme vyjádření souřadnic bodů X[x; y] této přímky v závislosti na parametru t.
Jak se počítá velikost vektoru
Výpočet velikosti vektoru je odvozen z výpočtu přepony pomocí Pythagorovy věty. Velikost vektoru u značíme absolutní hodnotou |u|. Častou chybou při výpočtu velikosti vektoru je nesprávné umocňování záporného čísla.
Jak se počítá odchylka přímek
Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.
Co je parametrická funkce
Parametrizace, parametrické vyjádření neboli parametrické rovnice geometrického útvaru (křivky, plochy) je zobrazení v matematice, které určuje souřadnice bodů tohoto útvaru jako funkce parametru. Opakem je implicitní rovnice útvaru například v podobě F(x,y) = 0.
Jak napsat parametrickou rovnici roviny
Analytická geometrieParametrickou rovnici roviny určíme podle definice. Pro u = B – A, v = C – A je rovnice roviny ABC: X = A + su + tv; s, t ∈ .Nejprve určíme vektory u = AB a v = AC. u = (-1; 1; 1), v = (4; -3; 2) a rovnici roviny vyjádříme jako: x = -s + 4t, y = 2 + s – 3t, z = 1 + s + 3t; s, t ∈ .
Jak najít kolmou rovinu
Kolmost dvou rovin
Dvě roviny jsou kolmé, pokud je jejich odchylka rovna 90°. Dvě roviny jsou kolmé, pokud jedna z nich obsahuje přímku, která je kolmá k druhé rovině.
Co platí pro dva obecně rovnoběžné vektory
jsou rovnoběžné právě tehdy, je-li vektor n = (a; b) nenulovým reálným násobkem vektoru n' = (a'; b'); jsou totožné právě tehdy, když je jedna rovnice násobkem druhé; jsou různoběžné právě tehdy, když má soustava jejich obecných rovnic právě jedno řešení.
Jak zjistit zda bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Jak se počítá směrnice přímky
Směrnice přímky se rovná „změna y dělená změnou x“.
Jak zjistit zda jsou vektory rovnoběžné
jsou rovnoběžné právě tehdy, je-li vektor n = (a; b) nenulovým reálným násobkem vektoru n' = (a'; b'); jsou totožné právě tehdy, když je jedna rovnice násobkem druhé; jsou různoběžné právě tehdy, když má soustava jejich obecných rovnic právě jedno řešení.
Jak zjistit Rovnobeznost vektoru
Dva vektory a, b jsou rovnoběžné právě tehdy, když jeden z nich je násobkem druhého, tj. když existuje takové reálné číslo k, že platí a = kb .
Jak určit odchylku dvou rovin
Odchylka dvou rovin je rovna odchylce jejich průsečnic s třetí rovinou, která je k oběma rovinám kolmá.
Co je odchylka dvou přímek
Definice odchylky přímek v planimetrii:
Odchylka dvou různoběžných přímek je velikost každého z ostrých nebo pravých úhlů, které spolu přímky svírají. Odchylka dvou rovnoběžných přímek je 0°.
Jak zapsat parametrickou rovnici
Každou přímku lze zapsat nějakým parametrickým vyjádřením a každé parametrické vyjádření popisuje nějakou přímku. Když parametrickou rovnici přímky p(A, u), kde A[a1; a2] a u = (u1; u2), zapíšeme pomocí souřadnic, získáme vyjádření souřadnic bodů X[x; y] této přímky v závislosti na parametru t.
Jak ovlivnuje vzhled grafu parametr a
Kladné hodnoty parametru a znamenají tvar „ďolíku“, záporné tvar „kopečku“. Čím je větší absolutní hodnota parametru a, tím je graf užší.
Kdy jsou dvě roviny kolmé
Definice: Dvě roviny jsou kolmé, jestliže jejich odchylka je 90°. Kritérium kolmosti dvou rovin: Obsahuje-li rovina σ přímku p kolmou k rovině ρ, pak jsou roviny σ, ρ k sobě kolmé. Definice: Je-li přímka p kolmá k rovině ρ, pak její odchylka od ρ je 90°.
Jak vypočítat průsečík dvou přímek
X = Q + sv, pro nějakou hodnotu parametrů t, s. Pokud hledáme průsečík těchto přímek, hledáme hodnoty parametrů t a s, pro které obě přímky určují stejný bod. Řešíme tedy rovnici P + tu = Q + sv.
Jak vypočítat Směrnicový tvar
Když to shrneme, každou přímku, která není rovnoběžná s osou y můžeme napsat ve tvaru y = kx + q, kde k, y ∈ ℝ a každou přímku rovnoběžnou s osou y můžeme napsat ve tvaru x = m, kde m ∈ ℝ. Rovnici ve tvaru y = kx + y se pak říká směrnicový tvar přímky a koeficient k nazýváme směrnicí přímky.