Jak se označuje polopřímka
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme ↦ A B \mapsto AB ↦AB.
Archiv
Jak se značí přímka v geometrii
Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.
ArchivPodobné
Kdy jsou Polopřímky opačně
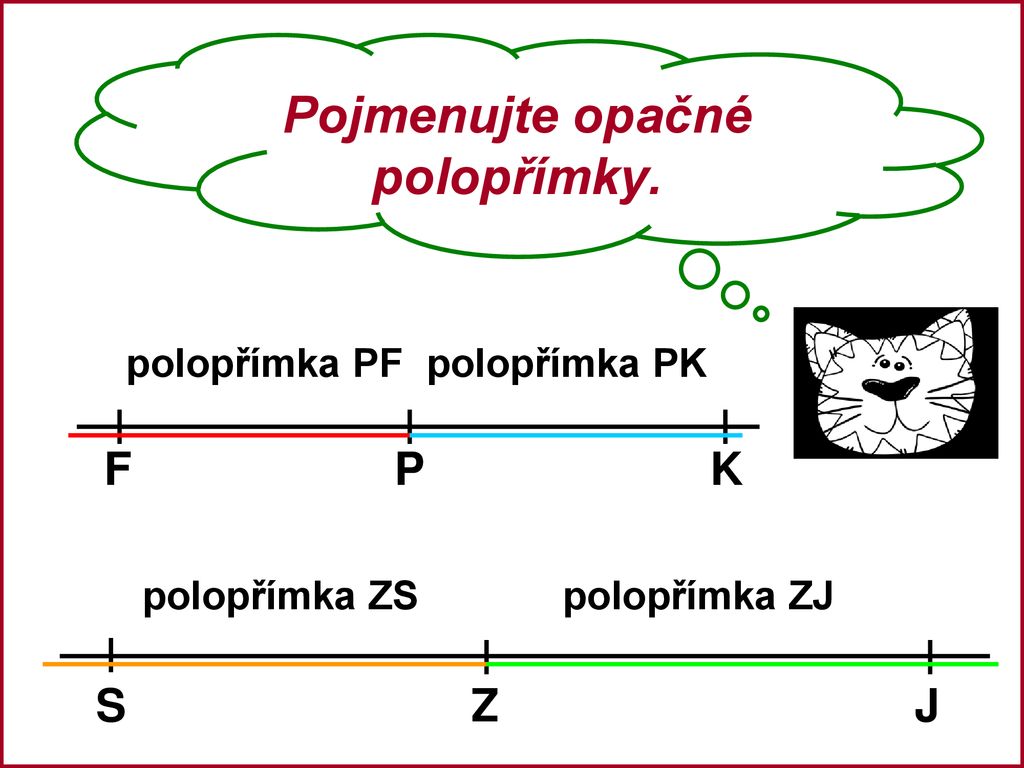
Opačná polopřímka k dané polopřímce je polopřímka, která leží na stejné přímce, má s danou polopřímkou stejný počáteční bod, ale opačný směr. Pro rozlišení směru se také používá šipka směřující opačným směrem, tzn. A C → je opačná polopřímka k A B → .
Jak vypadá úsečka
Úsečka se znázorňuje rovnou čarou mezi jejími krajními body, zapisuje se pomocí svých krajních bodů, případně malým písmenem.
Jak vypadá přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Jak značíme Polorovinu
Polorovinu lze znázornit např. pomocí rovnoběžného promítání, polorovina se zapisuje pomocí hraniční přímky a pomocného bodu se symbolem šipka. Opačná polorovina k dané polorovině je polorovina, která leží ve stejné rovině, má s danou polorovinou stejnou hraniční přímku, ale opačný směr.
Jak zjistit rovnici přímky
Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jak se označují body
Body značíme křížkem nebo krátkou čárkou, jestliže bod leží na čáře. Body označujeme velkými tiskacími písmeny.
Jak se dělá přímka
Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jak zjistit střed úsečky
Pomocí souřadnic dokážeme určit i souřadnice středu úsečky. Bod S ∈ AB je středem úsečky AB, právě tehdy, když platí |AS| = |BS|. V rovině pro souřadnice středu S[s1; s2] úsečky s krajními body A[a1; a2] a B[b1; b2] platí vztahy: s_{1} = \dfrac{a_{1} + b_{1}}{2}, s_{2} = \dfrac{a_{2} + b_{2}}{2}.
Co je to rovina a Polorovina
Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Přímka, která rozdělila rovinu, se nazývá hraniční přímka poloroviny. Pro bližší určení poloroviny se v polorovině volí další bod neležící na hraniční přímce, tento bod se nazývá pomocný bod.
Jak zjistit jestli body lezi na jedne přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. AB = (1; -2; 2), AC = (-1; 2; -1).
Jak vypada Polorovina
Polorovina je část roviny určená hraniční přímkou a aspoň jedním vnitř- ním bodem. Úsečka je část přímky ohraničená dvěma body (krajní body). Též můžeme říci, že je to přímá spojnice těchto dvou bodů. Úhel je část roviny ohraničená dvěma polopřímkami (ramena úhlu) se společným počátkem (vrchol úhlu).
Jak zjistit zda bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Jak se počítá směrnice přímky
Směrnice přímky se rovná „změna y dělená změnou x“.
Co znamená v geometrii s
trojúhelník ABC Bod S je průnikem (průsečíkem) přímek p, q.
Jak se zapisují úhlopříčky
Většinou se zapisuje v palcích (″) a nezahrnuje různě široké rámečky obrazovky, takže je konečná velikost zařízení zpravidla o něco větší. Úhlopříčka (a tedy velikost) je dána výškou a současně šířkou, tedy dvěma číselnými údaji, které zároveň udávají poměr stran.
Co znamená když je přímka kolmá
Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Jak se dělá osa úsečky
Narýsuj dvě shodné kružnice (stejný poloměr) o poloměru větším než polovina úsečky a se středy v krajních bodech úsečky. Následně spoj body, kde se obě kružnice protínají (průsečíky). Vzniklé úsečce (resp. přímce, na níž leží) se říká osa úsečky.
Jak vypočítat souřadnice středu úsečky
Pomocí souřadnic dokážeme určit i souřadnice středu úsečky. Bod S ∈ AB je středem úsečky AB, právě tehdy, když platí |AS| = |BS|. V rovině pro souřadnice středu S[s1; s2] úsečky s krajními body A[a1; a2] a B[b1; b2] platí vztahy: s_{1} = \dfrac{a_{1} + b_{1}}{2}, s_{2} = \dfrac{a_{2} + b_{2}}{2}.
Jak se počítá odchylka přímek
Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.
Co to je rovina
Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Jinak řečeno jde o dvoudimenzionální afinní prostor.
Jak vypočítat průsečík dvou přímek
X = Q + sv, pro nějakou hodnotu parametrů t, s. Pokud hledáme průsečík těchto přímek, hledáme hodnoty parametrů t a s, pro které obě přímky určují stejný bod. Řešíme tedy rovnici P + tu = Q + sv.
Co znamená ∈
Zároveň si naznačíme, jak vypadá axiomatická teorie množin. Základní (a vlastně jedinou) vlastností množin je, že mají prvky. Píšeme a ∈ A, což znamená, že a je prvkem množiny A. Malá a velká písmena používáme pro názornost; ve skutečnosti v teorii množin není nic jiného než množiny, t.j., i a je množina.
Kdo vymyslel geometrii
n. l.) a starém Egyptě (1 200 př. n. l.). Za zakladatele deskriptivní geometrie v dnešním slova smyslu je považován Gaspard Monge (1746–1818), který v díle Géometrie descriptive (1799) popsal kolmé promítání na dvě kolmé průmětny (Mongeovo promítání).