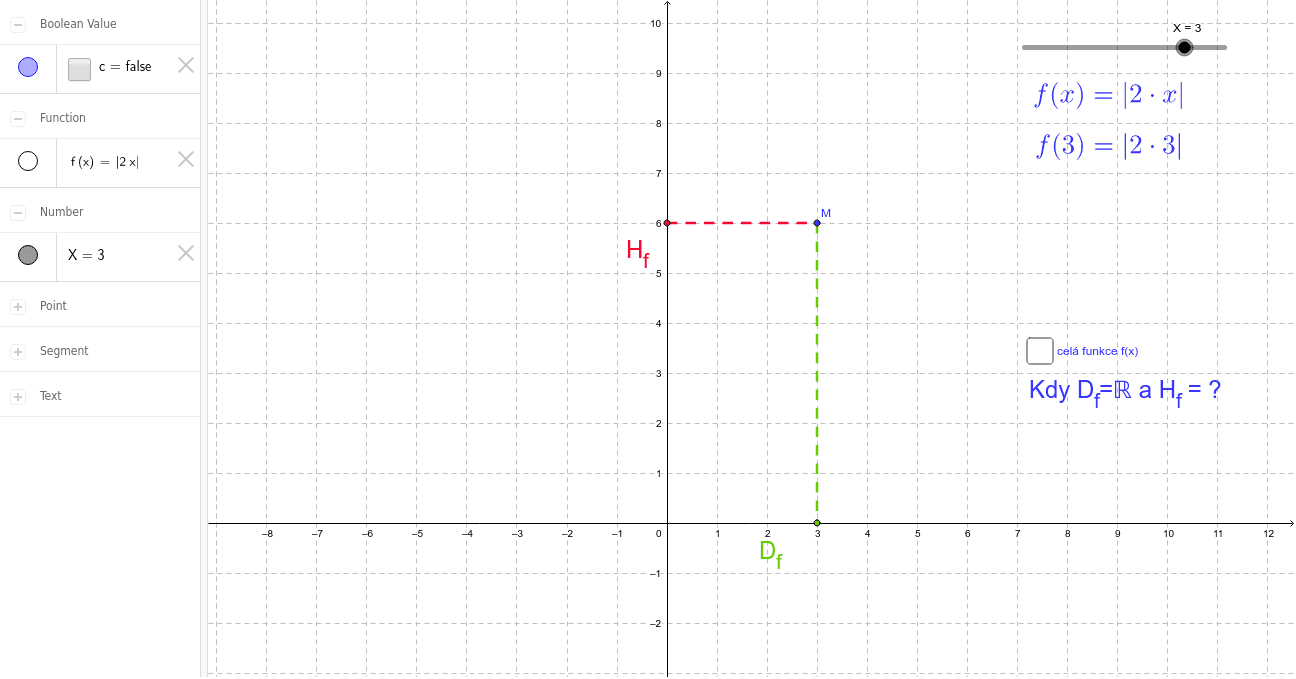
Jak poznat definiční obor
Definiční obor funkce je množina všech hodnot (čísel), kterých může proměnná x nabývat. Definiční obor funkce, kterou si pojmenujeme f, budeme značit D(f). Kdybychom si funkci pojmenovali jinak, například brrr, tak její definiční obor budeme značit D(brrr).
Archiv
Co nesmí být pod odmocninou
Ve funkčním předpisu první zadané funkce je lomený výraz, je proto potřeba stanovit definiční obor tak, aby nemohla nastat situace, kdy bude ve jmenovateli nula. Ve druhém případě bude ve funkčním předpisu funkce proměnná pod odmocninou, výraz pod odmocninou tedy nesmí být záporný.
Jak zapsat obor hodnot
Funkční hodnoty pro všechna x\in D(f) nabývají hodnot všech reálných čísel, obor hodnot zapíšeme jako H(f)=\mathbb R.
Co je definiční obor lineární funkce
Definiční obor lineární funkce je celá množina reálných čísel. Speciálním případem lineární funkce je funkce konstantní.
Co je f x
Značení y = f (x) znamená, že k hodnotě argumentu x přiřazuje funkce f hodnotu y. Někdy se také používá značení f : x ↦ y, slovy, funkce f posílá x na y. Nejobvyklejší způsob, jak zadat toto přiřazování, je pomocí nějakého vzorce, tj.
Co je to Arcsin
Arcsin, neboli arcus sinus je inverzní funkce k funkci sinus. Její argument musí být z intervalu -1 až 1 včetně.
Jak se částečně Odmocnuje
Jak částečně odmocňovatkrok. Číslo pod odmocninou přepíšeme na součin dvou činitelů (dvou čísel). Jedno je největší možná druhá mocnina:krok. Odmocninu součinu zapíšeme jako součin dvou odmocnin:krok. První odmocninu (z druhé mocniny) odmocníme a výsledek píšeme jako součin celého čísla a „zbytkové” odmocniny:
Jak přepsat odmocninu
Odmocninu n√a z nezáporného čísla a umocníme tak, že umocníme její základ a a získanou mocninu am odmocníme. Odmocninu n√a z nezáporného čísla a odmocníme tak, že její základ a odmocníme součinem odmocnitelů m⋅n.
Co to je definiční obor
Definiční obor funkce nám udává, co všechno do funkce můžeme dosadit. Například definiční obor funkce f(x)=x² jsou všechna reálná čísla a definiční obor funkce g(x)=1/x jsou všechna reálná čísla kromě x=0.
Jak poznat že je funkce omezená
Ekvivalentně, funkce f je omezená jestliže existuje číslo h takové, že pro všechna x z definičního oboru D( f ) platí -h ≤ f (x) ≤ h, jinými slovy | f (x)| ≤ h. Omezenost shora znamená, že existuje vodorovná čára tak, že celý graf funkce leží pod ní.
Jak se počítá lineární funkce
Lineární funkce je dána předpisem y = ax + b (a a b jsou reálná čísla). Grafem je přímka, která prochází body o souřadnicích [0; b], [1; a + b]. Pokud je a > 0 – funkce je rostoucí. Pokud je a < 0 – funkce je klesající.
Co je to Arctg
Vrátí arkustangens (inverzní funkce k funkci tangens) zadaného čísla. Arkustangens je úhel, jehož tangens je zadané číslo. Výsledný úhel je udáván v radiánech v intervalu -pí/2 až pí/2.
Kdy je síň 0
Sinus a kvadranty
| Stupně | Radiány | sin (x) |
|---|---|---|
| 0° | 0 | 0 |
| 90° | π/2 | 1 |
| 180° | π | 0 |
| 270° | 3π/2 | −1 |
Jak Odmocnit na třetí
Odmocňovat třetí odmocninou můžeme snadno takové mocniny deseti, které mají počet nul (mocniny větší než 1) nebo počet desetinných míst (mocniny menší než 1) dělitelný třemi. Odmocněním se počet nul (počet desetinných míst) zmenší na třetinu.
Jak rozložit odmocninu
Jak částečně odmocňovatkrok. Číslo pod odmocninou přepíšeme na součin dvou činitelů (dvou čísel). Jedno je největší možná druhá mocnina:krok. Odmocninu součinu zapíšeme jako součin dvou odmocnin:krok. První odmocninu (z druhé mocniny) odmocníme a výsledek píšeme jako součin celého čísla a „zbytkové” odmocniny:
Jak násobit mocniny
Násobení mocnin
Mocniny násobíme tak, že základ opíšeme a exponenty sečteme.
Co je umocnit
Umocňování je matematická operace, která vyjadřuje opakované násobení. Umocňování je k násobení v podobném vztahu, v jakém je samo násobení ke sčítání. Umocňování slouží ke zkrácenému zápisu vícenásobného násobení: V tomto vzorci se z označuje jako základ mocniny (mocněnec) a n se nazývá exponent (mocnitel).
Kdy je funkce omezená
Jestliže je funkce omezená shora, znamená to, že funkční hodnoty nepřekročí určitou horní hranici. V případě, že je funkce omezená zdola, pak všechny funkční hodnoty neklesnou pod určitou dolní hranici. Jestliže je funkce omezená shora i zdola, pak řekneme, že je to funkce omezená.
Kdy je funkce klesající
Funkce je klesající tehdy, když s rostoucí hodnotou x klesá hodnota y. Funkce f je klesající, právě když pro všechna x_1,x_2\in D(f) platí: Je-li x_1 < x_2, pak f(x_1) > f(x_2).
Jak poznat o jakou funkci se jedná
U lineární funkce, když máme nějakou změnu x, která je stejná, když se nám x mění o nějakou stejnou hodnotu, tak se nám i y musí měnit o stejnou hodnotu, ta změna musí být konstantní. Pokud se při změně x mění y o stále stejnou hodnotu, pak se jedná o lineární funkci.
Jak poznat co je funkce
Funkce je předpis, který každému číslu x z definičního oboru M přiřadí právě jedno y z oboru hodnot N. Funkci obvykle zapisujeme ve tvaru y = f(x), či ji můžeme vyjádřit explicitně f:y = x kde proměnná x je argument funkce.
Jak vypočítat inverzní funkci
Předpis inverzní funkce získáme tak, že se pokusíme vyjádřit x jako funkci argumentu y. Inverzní funkce k prosté funkci f je funkce f^{-1}, pro kterou platí: D(f^{-1})=H(f) a zároveň každému y\in D(f^{-1}) je přiřazeno právě to x\in D(f), pro které je f(x)=y.
Kdy je sinus kladný
V prvním kvadrantu mají funkce sinus, kosinus i tangens (kotangens) kladnou hodnotu. Sinus je kladný ještě v kvadrantu druhém, tangens ve třetím a kosinus ve čtvrtém.
Kdo vymyslel sinus
Snad jako první se studiu goniometrických funkcí a počítání jejich hodnot věnoval Hipparchos z Nikaje (180–125 př. n. l.), který porovnával délky oblouku kružnice při daném středovém úhlu (αr) s délkami jim odpovídajících tětiv (2r sin(α/2)).
Co je to mocnina
Umocňování je matematická operace, která vyjadřuje opakované násobení. Umocňování je k násobení v podobném vztahu, v jakém je samo násobení ke sčítání. Umocňování slouží ke zkrácenému zápisu vícenásobného násobení: V tomto vzorci se z označuje jako základ mocniny (mocněnec) a n se nazývá exponent (mocnitel).