Jak se zapisuje polopřímka
Polopřímka se znázorňuje rovnou čarou jdoucí od počátečního bodu přes pomocný bod dále, zapisuje se pomocí počátečního a pomocného bodu, např. A B → .
Archiv
Jak se značí přímka v zápisu
Přímka se obvykle zapisuje pomocí malých tiskacích písmen, například a. Přímka se obvykle zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku.
Archiv
Jak zapsat Polorovinu
Značení Polorovinu lze znázornit např. pomocí rovnoběžného promítání, polorovina se zapisuje pomocí hraniční přímky a pomocného bodu se symbolem šipka. Opačná polorovina k dané polorovině je polorovina, která leží ve stejné rovině, má s danou polorovinou stejnou hraniční přímku, ale opačný směr.
Jak se značí opačné Polopřímky
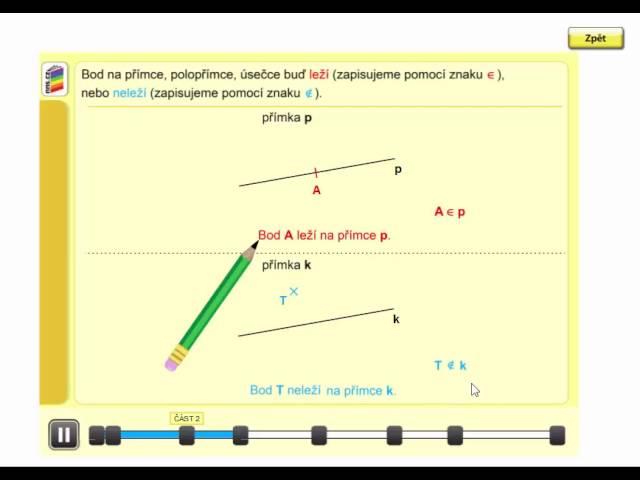
Zápisy pro polohu bodů na přímce jsou stejné jako u úseček. Kromě znaku AB ↔ pro přímku AB používáme podobný znak AB ֏ pro polopřímku AB. Přímka AB je totožná s přímkou p (nebo přímka AB splývá s přímkou p).
Jak vypadá přímka p
Lze tedy tedy přímka změřit POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Jak se dělá přímka
Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jak zjistit rovnici přímky
Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jaký je rozdíl mezi přímkou a Polopřímkou
Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem. Your browser does not support this audio format. Polopřímka – je podobná přímce, má počátek (ale stále nemá konec).
Jak vypada Polorovina
Polorovina je část roviny určená hraniční přímkou a aspoň jedním vnitř- ním bodem. Úsečka je část přímky ohraničená dvěma body (krajní body). Též můžeme říci, že je to přímá spojnice těchto dvou bodů. Úhel je část roviny ohraničená dvěma polopřímkami (ramena úhlu) se společným počátkem (vrchol úhlu).
Co to je Polopřímka
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme ↦ A B \mapsto AB ↦AB. Každý bod rozděluje přímku na dvě opačné polopřímky se společným počátečním bodem.
Jak se vyznačuje přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Jaký je rozdíl mezi přímkou a úsečkou
Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. Co nám tedy na obrázku vyznačuje šipka Lze tedy polopřímku změřit ÚSEČKA je rovná čára, která má dva krajní body (značíme velkými tiskacími písmeny
Co znamená když je přímka kolmá
Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Jak zapsat přímku
Libovolnou přímku můžeme zapsat jako p ( A , u → ) , kde A je bod ležící na přímce a je vektor rovnoběžný s přímkou. Například přímku p1 bychom mohli napsat ve tvaru p ( G , u → ) a přímku p2 jako p ( E , u → ) nebo p ( F , u → ) — můžeme použít jakýkoliv bod ležící na přímce.
Jak vypadá přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Co je jedna Polorovina
Polorovina je část roviny určená hraniční přímkou a aspoň jedním vnitř- ním bodem. Úsečka je část přímky ohraničená dvěma body (krajní body). Též můžeme říci, že je to přímá spojnice těchto dvou bodů.
Jak se označují přímky
Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.
Jak se dělá kolmá přímka
Kolmici lze v rovině (třeba na papíře) nejsnadněji narýsovat pomocí trojúhelníku s ryskou a to tak, že se ryska přiloží na přímku a podle hrany trojúhelníku narýsujeme kolmici k této přímce. Jde to ale také pomocí kružítka a pravítka nebo trojúhelníku bez rysky.
Jak určit vzájemnou polohu přímky a roviny
V prostoru rozlišujeme tři možné vzájemné polohy roviny ρ a přímky p.p ∩ ρ = ∅ Přímka p je s rovinou ρ rovnoběžná různá. Přímka a rovina nemají žádný společný bod.p ∩ ρ = {P} Přímka p a rovina ρ jsou různoběžné. Přímka rovinu protíná v jednom bodě, bodě P.p ∩ ρ = p Přímka p leží v rovině ρ.
Jak se počítá směrnice přímky
Směrnice přímky je číslo měřící strmost dané přímky. Matematicky směrnici spočítáme jako "změna y dělená změnou x" (přesněji změna y-ové souřadnice dělená změnou x-ové souřadnice při přechodu mezi dvěma libovolnými body ležícími na dané přímce).
Jak zjistit jestli bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Jak se zapisují úsečky
Značení Úsečka se znázorňuje rovnou čarou mezi jejími krajními body, zapisuje se pomocí svých krajních bodů, případně malým písmenem.
Jak zjistit zda jsou přímky totožné
Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.
Jak zjistit zda bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Jak vypočítat směrový úhel přímky
Když to shrneme, každou přímku, která není rovnoběžná s osou y můžeme napsat ve tvaru y = kx + q, kde k, y ∈ ℝ a každou přímku rovnoběžnou s osou y můžeme napsat ve tvaru x = m, kde m ∈ ℝ. Rovnici ve tvaru y = kx + y se pak říká směrnicový tvar přímky a koeficient k nazýváme směrnicí přímky.