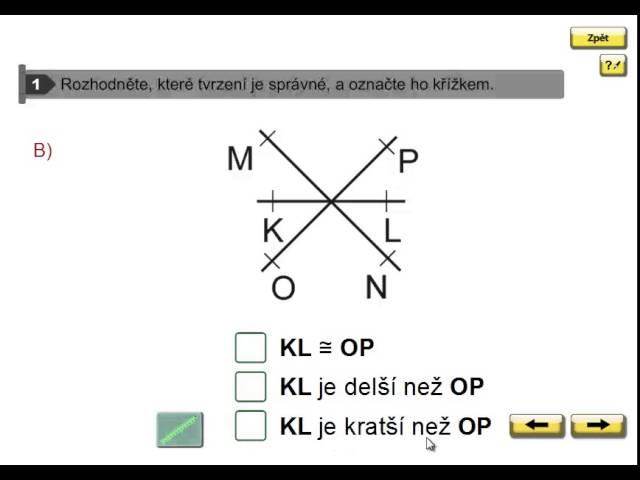
Co to je shodná úsečka
Říkáme, že úsečka AB je shodná s úsečkou CD tehdy, pokud jednu úsečku můžeme přenést na druhou tak, že se tyto úsečky navzájem překrývají. Shodnost úseček značíme symbolem ≅ (obr.
Archiv
Kdy jsou shodné dvě úsečky
Dvě úsečky jsou shodné, když mají stejnou délku.
Jaký je rozdíl mezi přímkou a úsečkou
Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. Co nám tedy na obrázku vyznačuje šipka Lze tedy polopřímku změřit ÚSEČKA je rovná čára, která má dva krajní body (značíme velkými tiskacími písmeny
Co to je osa úsečky
Střed úsečky je bod, který leží na úsečce a jehož vzdálenost od obou krajních bodů je stejná. Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.
Co to je shodnost
Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost.
Jak zjistit střed úsečky
Pomocí souřadnic dokážeme určit i souřadnice středu úsečky. Bod S ∈ AB je středem úsečky AB, právě tehdy, když platí |AS| = |BS|. V rovině pro souřadnice středu S[s1; s2] úsečky s krajními body A[a1; a2] a B[b1; b2] platí vztahy: s_{1} = \dfrac{a_{1} + b_{1}}{2}, s_{2} = \dfrac{a_{2} + b_{2}}{2}.
Co to je bod
Bod je bezrozměrný základní geometrický útvar. Dle Euklidových Základů je bod něco, co nemá části, tedy to co již nelze dále dělit. Bod časoprostoru se nazývá událost.
Jak se dělá osa úsečky
Narýsuj dvě shodné kružnice (stejný poloměr) o poloměru větším než polovina úsečky a se středy v krajních bodech úsečky. Následně spoj body, kde se obě kružnice protínají (průsečíky). Vzniklé úsečce (resp. přímce, na níž leží) se říká osa úsečky.
Jak se značí úsečky
Úsečka je vyznačena dvěma krajními body, které jsou spojeny rovnou čárou. Úsečku označujeme krajními body, takže můžeme mluvit o úsečce AB, pokud má krajní body A a B. U úsečky můžeme měřit délku, což je vzdálenost mezi jejími krajními body. Pokud mluvíme o délce úsečky AB, zapisujeme to pomocí svislítek: |AB|.
Co jsou to shodné útvary
Jestliže dva rovinné útvary můžeme přemístit tak, že se kryjí,budeme je nazývat shodnými útvary. Jestliže se dva trojúhelníky shodují ve všech třech stranách, pak jsou shodné. Jestliže se dva trojúhelníky shodují ve dvou stranách a úhlu jimi sevřeném, pak jsou shodné.
Jak vypočítat souřadnice středu úsečky
Pomocí souřadnic dokážeme určit i souřadnice středu úsečky. Bod S ∈ AB je středem úsečky AB, právě tehdy, když platí |AS| = |BS|. V rovině pro souřadnice středu S[s1; s2] úsečky s krajními body A[a1; a2] a B[b1; b2] platí vztahy: s_{1} = \dfrac{a_{1} + b_{1}}{2}, s_{2} = \dfrac{a_{2} + b_{2}}{2}.
Co to je kolmice
Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Jak se oznacuje bod
Bod – je základní geometrický pojem, bod obvykle označujeme křížkem a značíme jej velkým písmenem. Your browser does not support this audio format. Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.
Jak zjistím osu úhlu
Tam, kde se kružnice protnou, se nachází jeden bod osy, bod označíme O. Druhý bod osy se nachází ve vrcholu úhlu. Skrze tyto body povedete přímku a máte osu.
Co znamená osa úhlu
Osa úhlu rozděluje úhel na dva stejně velké úhly. Je množinou všech bodů, které mají stejnou vzdálenost od obou ramen úhlu.
Jak se počítá střed úsečky
Střed úsečky v rovině
Střed dělí, jak už jsme si řekli, úsečku na dvě stejné části. Z toho vyplyne vzorec: S[(a1+b1)/2; (a2+b2)/2] .
Co je to Poloprimka
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme ↦ A B \mapsto AB ↦AB. Každý bod rozděluje přímku na dvě opačné polopřímky se společným počátečním bodem.
Jak se zapisují úhlopříčky
Většinou se zapisuje v palcích (″) a nezahrnuje různě široké rámečky obrazovky, takže je konečná velikost zařízení zpravidla o něco větší. Úhlopříčka (a tedy velikost) je dána výškou a současně šířkou, tedy dvěma číselnými údaji, které zároveň udávají poměr stran.
Jak se sčítají úhly
Při sčítání a odčítání úhlů sčítáme a odčítáme zvlášť stupně, zvlášť minuty a zvlášť vteřiny. Př. 1 Sečti nebo odečti úhly. V případě, že počet minut po sečtení překročí hodnotu 60, odečteme od hodnoty v minutách číslo 60 a k hodnotě stupňů přičteme 1 stupeň.
Jak vypočítat vzdálenost dvou bodů
Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.
Jak se počítá počet úhlopříček
Úsečka spojující dva nesousední vrcholy se nazývá úhlopříčka. Úhlopříčky existují v n-úhelníku pro n > 3 a platí, že počet úhlopříček je ½ ∙ n ∙ (n – 3).
Jak vypadá úhlopříčka
Úhlopříčka je tak úsečka, která spojuje dva protilehlé vrcholy čtverce. Další fakta o úhlopříčkách: Úhlopříčka e vžjdy delší než strana čtverce. Přesněji: pokud má strana čtverce délku a, pak úhlopříčka u má délku | u | = a ⋅ 2 .
Jak se počítají stupně
Jeden stupeň má 60 minut a minuta se dále dělí na 60 vteřin, tedy stupeň má 3 600 vteřin: 1° = 60′ = 3600″ Úhlové stupně se používají mimo jiné ve sférických soustavách souřadnic, ke kterým patří zeměpisné souřadnice a různé systémy používané v astronomii.
Jak se dělí úhly
Druhy úhlůNulový úhel (0°, 0 rad) je úhel, jehož ramena leží na sobě.Ostrý úhel (< 90°, < /2 rad) je úhel menší než pravý úhel.Pravý úhel (90°, /2) je polovina přímého úhlu.Tupý úhel (> 90°, ale < 180°) je úhel větší než pravý úhel, ale menší než přímý úhel.Přímý úhel (180°,Plný úhel (360°, 2.
Jak určit vzdálenost bodu
Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.