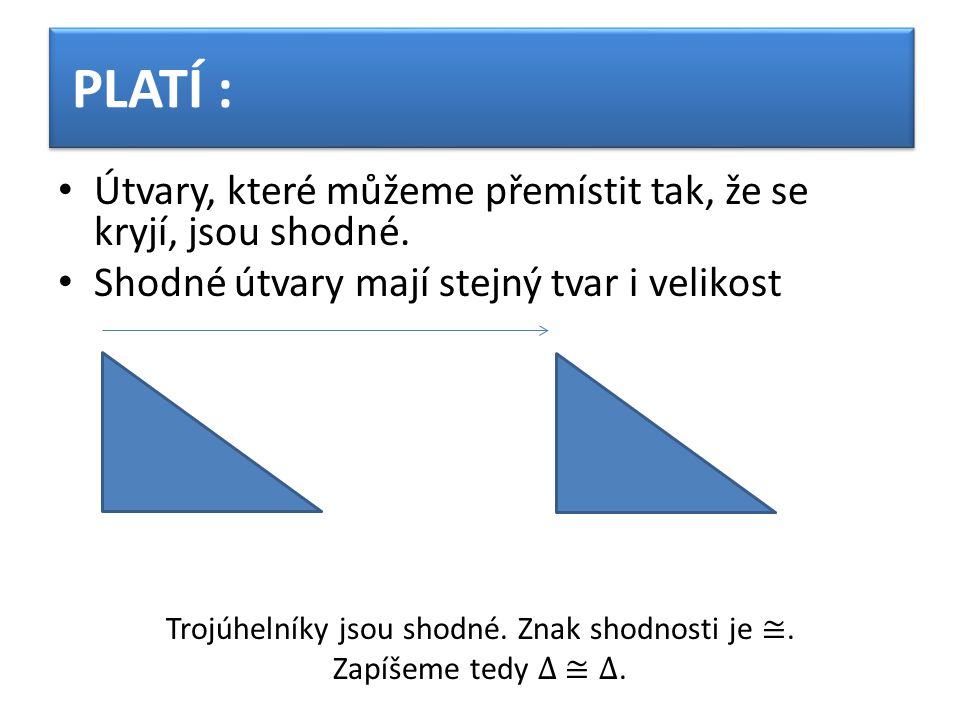
Co jsou to shodné útvary
Jestliže dva rovinné útvary můžeme přemístit tak, že se kryjí,budeme je nazývat shodnými útvary. Jestliže se dva trojúhelníky shodují ve všech třech stranách, pak jsou shodné. Jestliže se dva trojúhelníky shodují ve dvou stranách a úhlu jimi sevřeném, pak jsou shodné.
Archiv
Jak se Znaci shodnost
Shodnost je takové zobrazení, ve kterém platí, že když se zobrazí jedna úsečka na druhou (AB na A'B'), tak mají stejnou velikost (jsou shodné). Zapisujeme: AB =~A'B' Platí, že ve shodnosti se zachovává velikost stran a velikost úhlů (tzn. rovnoběžky se zobrazí na rovnoběžky, kolmice na kolmice …).
Co je to Samodružný bod
Samodružný bod zobrazení f je takový bod X, který se zobrazí sám na sebe, tj. f(X)=X. Samodružná přímka zobrazení f je taková přímka p, která se zobrazí sama na sebe, tj. f(p)=p.
Co patří do shodných zobrazení
Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost.
Co znamená že úsečky jsou shodné
Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček.
Jak se dělá osova Soumernost
Zápisem O(o): X \rightarrow X' budeme rozumět, že bod X' je obrazem bodu X v osové souměrnosti s osou o. Osová souměrnost je nepřímá shodnost. Osová souměrnost je jednoznačně určena osou souměrnosti nebo dvojicí nesplývajících bodů X, X', kde bod X je vzor a bod X' je obraz bodu X.
Co to je osa v geometrii
Osa, též symetrála, je přímka určující souměrnost množiny bodů nebo tělesa. Množina bodů je osově souměrná podle přímky p, jestliže s každým bodem obsahuje také jeho obraz souměrný podle osy p. Dva body jsou souměrné podle dané osy, jestliže jimi určená úsečka je kolmá na osu a její střed leží na ose.
Co je to středová souměrnost
Středová souměrnost S(S) se středem v bodě S je zobrazení v rovině, ve kterém se zobrazí bod S na bod S'=S a každý bod X \neq S na bod X' tak, že bod S je středem úsečky XX'. Tedy platí, že |XS|=|SX'|. Bod S se nazývá střed souměrnosti.
Co vznikne složením dvou osových Souměrností
Složením dvou osových souměrností se stejnou osou je identita. Složením dvou osových souměrností s různými rovnoběžnými osami je posunutí. Každé posunutí lze vyjádřit jako složení dvou osových souměrností. Složením dvou osových souměrností s různoběžnými osami je otočení kolem průsečíku os.
Kdy jsou úsečky shodné
Shodné úsečky mají stejnou délku.
Kdy jsou dvě úsečky shodne
Dvě úsečky jsou shodné, když mají stejnou délku. Př.
Jak určit osu souměrnosti
Osová souměrnost O(o) s osou o je zobrazení v rovině, ve kterém se zobrazí každý bod X \in o na bod X'=X a každý bod X \not\in o na bod X' tak, že úsečka XX' je kolmá na osu o a střed S úsečky XX' leží na přímce o. Tedy platí, že |XS|=|SX'|, kde bod S \in o. Přímka o se nazývá osa souměrnosti.
Jak udělat osu úsečky
Narýsuj dvě shodné kružnice (stejný poloměr) o poloměru větším než polovina úsečky a se středy v krajních bodech úsečky. Následně spoj body, kde se obě kružnice protínají (průsečíky). Vzniklé úsečce (resp. přímce, na níž leží) se říká osa úsečky.
Jak zjistím osu úhlu
Tam, kde se kružnice protnou, se nachází jeden bod osy, bod označíme O. Druhý bod osy se nachází ve vrcholu úhlu. Skrze tyto body povedete přímku a máte osu.
Jak poznat středově souměrný utvar
Středově souměrný útvar
Útvar označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu.
Co jsou shodná zobrazení
Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost. Z definice shodného zobrazení plyne, že každé shodné zobrazení je prosté.
Co je shodnost úseček
Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček.
Co to je shodná úsečka
Říkáme, že úsečka AB je shodná s úsečkou CD tehdy, pokud jednu úsečku můžeme přenést na druhou tak, že se tyto úsečky navzájem překrývají. Shodnost úseček značíme symbolem ≅ (obr.
Jak se dělá osa úsečky
Narýsuj dvě shodné kružnice (stejný poloměr) o poloměru větším než polovina úsečky a se středy v krajních bodech úsečky. Následně spoj body, kde se obě kružnice protínají (průsečíky). Vzniklé úsečce (resp. přímce, na níž leží) se říká osa úsečky.
Co to je osa
Osa, též symetrála, je přímka určující souměrnost množiny bodů nebo tělesa. Množina bodů je osově souměrná podle přímky p, jestliže s každým bodem obsahuje také jeho obraz souměrný podle osy p.
Co to je osa úsečky
Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.
Jak určit střed souměrnosti
Střed najdeme jako průsečík spojnic dvou k sobě náležících bodů. Nezáleží na tom, jakou dvojici k sobě náležících bodů si vybereme, všechny spojnice se protínají v jednom bodě.
Co je to středové souměrnost
Středová souměrnost S(S) se středem v bodě S je zobrazení v rovině, ve kterém se zobrazí bod S na bod S'=S a každý bod X \neq S na bod X' tak, že bod S je středem úsečky XX'. Tedy platí, že |XS|=|SX'|. Bod S se nazývá střed souměrnosti.
Co je to osa zlá
Osa zla (anglicky Axis of evil) je termín používaný bývalým prezidentem USA George W. Bushem. Podle něj jsou to státy, které napomáhají terorismu (např. tím, že poskytují zázemí teroristům a teroristickým organizacím) a vyrábějí zbraně hromadného ničení.
Co to je přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.