Jak zjistit vektor přímky
Každá přímka v rovině je určena dvěma různými body A a B. Tyto body určují také vektor. My tento vektor pojmenujeme a využijeme jej pro zavedení parametrického vyjádření přímky. Jestliže A, B jsou dva různé body, pak vektor u = B – A nazýváme směrový vektor přímky AB.
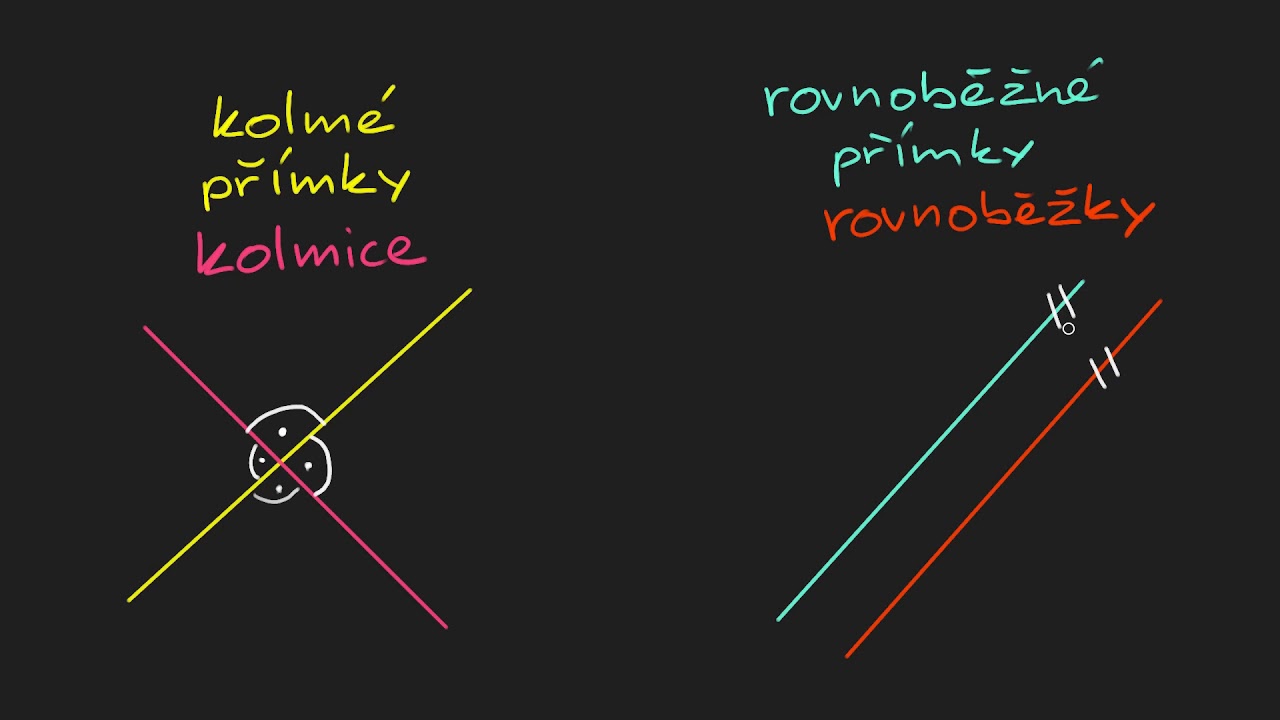
Kdy jsou přímky kolmé
Dvě přímky jsou k sobě kolmé právě tehdy, když jejich odchylka je 90°. ⇒ • Navzájem kolmé mohou být i mimoběžky. Dvě úsečky jsou kolmé, právě když leží na kolmých přímkách.
Jak poznat že body leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Co to je kolmá přímka
Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Jak najít kolmý vektor
3) dva vektory a , b jsou na sebe kolmé právě tehdy, když jejich skalární součin je roven nule. Vektorový součin je další operace s vektory.
Jak zjistit rovnici přímky
Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jak se počítá odchylka přímek
Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.
Jak vypadá přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Kdy jsou roviny kolmé
Definice: Dvě roviny jsou kolmé, jestliže jejich odchylka je 90°. Kritérium kolmosti dvou rovin: Obsahuje-li rovina σ přímku p kolmou k rovině ρ, pak jsou roviny σ, ρ k sobě kolmé. Definice: Je-li přímka p kolmá k rovině ρ, pak její odchylka od ρ je 90°.
Kdy jsou vektory na sebe kolmé
3) dva vektory a , b jsou na sebe kolmé právě tehdy, když jejich skalární součin je roven nule. Vektorový součin je další operace s vektory.
Jak se počítá směrnice přímky
Směrnice přímky se rovná „změna y dělená změnou x“.
Co je to odchylka přímky
Odchylka dvou různoběžných přímek je velikost každého z ostrých nebo pravých úhlů, které spolu přímky svírají. Odchylka dvou rovnoběžných přímek je 0°. Př. 1: Srovnej planimetrickou definici odchylky dvou přímek se stavem ve stereometrii a navrhni její stereometrickou definici.
Jak se vyznačuje přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Jak najít kolmou rovinu
Kolmost dvou rovin
Dvě roviny jsou kolmé, pokud je jejich odchylka rovna 90°. Dvě roviny jsou kolmé, pokud jedna z nich obsahuje přímku, která je kolmá k druhé rovině.
Jak zjistit odchylku rovin
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Jak se sčítají vektory
Jak bychom to udělali, kdybychom chtěli sečíst tyto dva vektory, tedy provést a plus b. A já vám teď prozradím, že to je úplně jednoduché. Sčítáme-li dva vektory, tak prostě a jednoduše sečteme jejich x-ové složky a jejich y-ové složky. A tak dostaneme výsledný vektor.
Jak vypočítat směrový úhel přímky
Když to shrneme, každou přímku, která není rovnoběžná s osou y můžeme napsat ve tvaru y = kx + q, kde k, y ∈ ℝ a každou přímku rovnoběžnou s osou y můžeme napsat ve tvaru x = m, kde m ∈ ℝ. Rovnici ve tvaru y = kx + y se pak říká směrnicový tvar přímky a koeficient k nazýváme směrnicí přímky.
Jakou odchylku mají dvě kolmé roviny
Definice: Dvě roviny jsou kolmé, jestliže jejich odchylka je 90°. Kritérium kolmosti dvou rovin: Obsahuje-li rovina σ přímku p kolmou k rovině ρ, pak jsou roviny σ, ρ k sobě kolmé. Definice: Je-li přímka p kolmá k rovině ρ, pak její odchylka od ρ je 90°.
Jak vypadá přímka p
Lze tedy tedy přímka změřit POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Kdy je přímka kolmá k rovině
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.
Čím je určen vektor
Vektory se ve fyzice obvykle popisují pomocí souřadnic, které ovšem závisí na volbě souřadnicových os. V matematice je někdy definován vektor jako uspořádaná n-tice prvků (typicky čísel), označovaných jako složky (též komponenty) vektoru.
Jak určit směrnici přímky
Směrnice přímky je číslo měřící strmost dané přímky. Matematicky směrnici spočítáme jako "změna y dělená změnou x" (přesněji změna y-ové souřadnice dělená změnou x-ové souřadnice při přechodu mezi dvěma libovolnými body ležícími na dané přímce).
Jaký je rozdíl mezi přímkou a úsečkou
Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. Co nám tedy na obrázku vyznačuje šipka Lze tedy polopřímku změřit ÚSEČKA je rovná čára, která má dva krajní body (značíme velkými tiskacími písmeny
Jak urcit směr vektoru
Směr vektoru c lze určit pomocí pravidla pravé ruky: Pokud směřuje vektor a ve směru ukazováku a vektor b ve směru prostředníku pravé ruky, potom vektor c vzniklý vektorovým součinem a×b směřuje ve směru palce, který je umístěn kolmo k dlani.
Co je to směrnice přímky
Směrnice přímky je číslo měřící strmost dané přímky. Matematicky směrnici spočítáme jako "změna y dělená změnou x" (přesněji změna y-ové souřadnice dělená změnou x-ové souřadnice při přechodu mezi dvěma libovolnými body ležícími na dané přímce).