
Kryptografia stanowi podstawę schematów podpisów cyfrowych kryptowalut i jest podstawą ich bezpiecznej weryfikacji transakcji między dwiema stronami w zdecentralizowanej sieci. Obecnie istnieje wiele metod kryptograficznych używanych przez różne kryptowaluty, koncentrując się na zapewnieniu wydajnych i bezpiecznych modeli transakcji.
Kryptografia krzywych eliptycznych (ECC) jest jedną z najczęściej stosowanych metod podpisów cyfrowych w kryptowalutach, a określony schemat, algorytm podpisu cyfrowego krzywej eliptycznej (ECDSA) jest stosowany zarówno w Bitcoin, jak i Ethereum do podpisywania transakcji.

Tło ECC i ECDSA
Kryptografia krzywych eliptycznych została zaproponowana niezależnie przez matematyków Neala Koblitza i Victora S. Millera w 1985 roku. Chociaż była to przełom w kryptografii, ECC nie była szeroko stosowana aż do wczesnych lat 2000, kiedy pojawił się Internet, kiedy rządy i dostawcy Internetu zaczęli go używać jako metoda szyfrowania.
W porównaniu z szyfrowaniem RSA, ECC oferuje znaczną przewagę. Rozmiar klucza używany do ECC jest znacznie mniejszy niż wymagany do szyfrowania RSA, a jednocześnie zapewnia ten sam poziom bezpieczeństwa. Chociaż szyfrowanie RSA jest obecnie szerzej stosowane w Internecie, ECC jest zasadniczo bardziej wydajną formą RSA, co jest jednym z głównych powodów, dla których jest używane w kryptowalutach.

Przeczytaj: Co to jest kryptografia RSA? Kompletny przewodnik po tym algorytmie szyfrowania
Amerykański Narodowy Instytut Standardów i Technologii (NIST) zatwierdza ECC jako „Apartament B”Zalecane algorytmy, a NSA oficjalnie wspiera klasyfikację ściśle tajnych informacji za pomocą 384-bitowych kluczy. Jako przykład efektywności ECC w porównaniu z RSA, ten sam 384-bitowy klucz używany do szyfrowania informacji niejawnych wymagałby 7680-bitowego klucza z szyfrowaniem RSA. Wydajność zapewniana przez ECC jest zatem niezwykle przydatna w sieciach blockchain, ponieważ zmniejsza rozmiar transakcji.
Jak to działa
Kryptografia krzywych eliptycznych jest metodą klucz publiczny szyfrowanie oparte na funkcji algebraicznej i strukturze krzywej na grafie skończonym. Wykorzystuje funkcję zapadni opartą na niemożności określenia dyskretnego logarytmu losowego elementu krzywej eliptycznej, który ma powszechnie znany punkt bazowy.
Funkcje pułapki są używane w kryptografii klucza publicznego, aby tak było, zaczynając od A -> B jest trywialne, ale idąc z B -> A jest niewykonalne, wykorzystując określony problem matematyczny. Na przykład szyfrowanie RSA opiera się na koncepcji Faktoryzacja podstawowa, a ESK opiera się na koncepcji Mnożenie punktów, gdzie mnożnik reprezentuje klucz prywatny i nie można go obliczyć na podstawie podanych punktów początkowych.
Krzywa eliptyczna musi składać się z punktów spełniających równanie:
y ^ 2 = ax ^ 3 + b
(x, y) na krzywej reprezentują punkt, podczas gdy a i b są stałymi. Teoretycznie istnieją nieskończone krzywe, które można by stworzyć, ale specjalnie zastosowane do kryptowalut (w przypadku Bitcoin i Ethereum), szczególna krzywa eliptyczna zwana secp256k1 Jest używane. Przedstawiono to na poniższym obrazku.
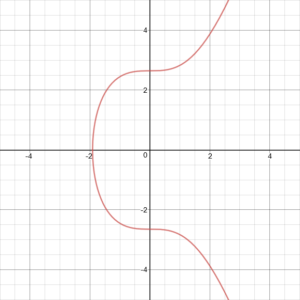
Jak widać, krzywe eliptyczne są symetryczne względem osi x. Z tego powodu, jeśli narysujesz linię prostą zaczynając od losowego punktu na krzywej, linia ta przecina krzywą w nie więcej niż 3 punktach. Rysujesz linię przez pierwsze dwa punkty i określasz, gdzie linia przecina się z trzecim punktem. Następnie odbij trzeci punkt na osi x (jest symetryczny), a ten punkt jest wynikiem dodania do siebie dwóch pierwszych punktów. Pokazuje to poniższy obrazek.

Na powyższym wykresie V i A reprezentują punkty początkowe, X to trzeci punkt, a ostatni punkt (nazwijmy go Z) reprezentuje dodanie V i A do siebie. W przypadku schematu podpisu cyfrowego punkt bazowy linii jest zwykle wstępnie zdefiniowany.
Aby ECC utworzyło funkcję zapadni, kryptografia krzywych eliptycznych wykorzystuje mnożenie punktów, gdzie znany punkt bazowy jest wielokrotnie dodawany do siebie. W takim przypadku użyjmy punktu bazowego P, którego celem jest znalezienie 2P, jak opisano poniżej.
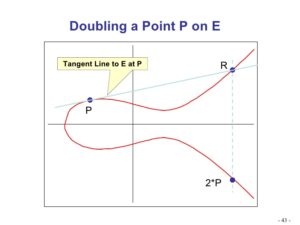
Powyżej styczna biegnie od punktu P do punktu R, który jest punktem przecięcia. Odbiciem tego punktu jest 2P. Załóżmy, że chcemy to kontynuować i znaleźć 3P, 4P i tak dalej. Następnie łączymy P i 2P, a następnie odzwierciedlamy ten punkt na skrzyżowaniu i kontynuujemy to dla 4P. Zilustrowane poniżej:
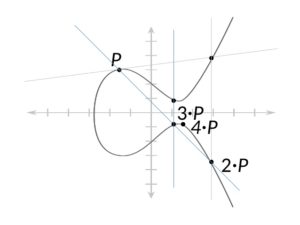
Jest to właściwość multiplikatywna wykresu, ponieważ znajdujemy punkty, które są pomnożeniem liczby całkowitej z samym punktem. Rezultatem jest to, co nadaje tej funkcji zapadnię, znaną jako problem z logarytmem dyskretnym.
Jeśli przedstawimy zmienną x jako 384-bitową liczbę całkowitą i pomnożymy ją przez punkt bazowy P, wynikiem będzie punkt na krzywej, zwany Z. W przypadku kryptowalut Z jest publiczne, ale oryginalna zmienna x jest tajna (prywatna klucz). Aby określić x na podstawie Z i P, musisz określić, ile razy P zostało dodane do siebie, aby uzyskać punkt Z na krzywej. Ten problem jest formą arytmetyka modularna jest to matematycznie niewykonalne i dlatego ESK jest tak bezpieczne.
Użyj w kryptowalutach
Analizując zapotrzebowanie na schematy podpisów cyfrowych w kryptowalutach, istnieją 4 podstawowe wymagania każdego schematu, które muszą być spełnione, aby schemat podpisu był autentyczny i weryfikowalny. Obejmują one:
- Powinno istnieć możliwość udowodnienia, że podpisujący transakcję jest sygnatariuszem.
- Podpis nie może być sfałszowany.
- Podpis musi być niezaprzeczalny, co oznacza, że podpisy są ostateczne i nie mogą być powiązane z inną tożsamością.
- Wyprowadzenie klucza prywatnego z odpowiedniego klucza publicznego powinno być niewykonalne obliczeniowo.
Kryptografia krzywych eliptycznych spełnia wszystkie 4 warunki i jest w tym szczególnie skuteczna. Używając ECC, współrzędne (x, y) punktu na wykresie byłyby twoim kluczem publicznym, a 384-bitowa losowa liczba całkowita x byłaby twoim kluczem prywatnym.
Możliwe jest również udowodnienie komuś, że znasz wartość x, bez faktycznego ujawniania, czym jest x. Ta właściwość dodatkowo pomaga spełnić warunki niezbędne do zrównoważonego użytkowania w schemacie transakcji podpisu cyfrowego.
Problemy kwantowe
Stosowanie ECC w schematach podpisu cyfrowego dla kryptowalut jest wyjątkowo bezpieczne. Jednak ostatnio pojawiły się obawy dotyczące przyszłego potencjału komputerów kwantowych i ich znacznej mocy, która może przełamać ECC. Chociaż uważa się, że jego możliwość jest oddalona o wiele lat, Algorytm Shora teoretycznie byłby w stanie obliczyć dyskretne logarytmy na hipotetycznym komputerze kwantowym o wystarczającej mocy.
Różne kryptowaluty przyjęły perspektywiczne podejście do potencjalnego zagrożenia stwarzanego przez komputery kwantowe, wdrażając algorytmy kwantowe jako podstawę swoich schematów podpisu cyfrowego. Nawet NSA w 2015 roku ogłosiła planowane przyszłe przejście z ECC na inny zestaw szyfrów dla potrzeb szyfrowania ze względu na zbliżającą się nieuchronność kwantowej mocy obliczeniowej.

Przeczytaj: Obliczenia kwantowe: jakie zagrożenie stwarza dla bitcoina?
W tym momencie obawy te są przede wszystkim spekulacjami, ponieważ moc obliczeniowa kwantowa niezbędna dla algorytmu Shora do obliczania logarytmów dyskretnych jest znacznie wyższa niż nawet w przypadku najpotężniejszych istniejących obecnie komputerów kwantowych wczesnego etapu.
Wniosek
Patrząc w przyszłość, kolejne generacje kryptowalut mogą ostatecznie przejść na bardziej zaawansowane metody szyfrowania w celu zabezpieczenia swoich transakcji i potencjalnie Bitcoin i Ethereum mogą wymagać tego samego przejścia.
Na razie ECC i inne schematy podpisu cyfrowego wykorzystujące funkcje zapadni pozostają jednymi z najbezpieczniejszych metod szyfrowania na świecie i powinny tak pozostać przez jakiś czas.


