
La cryptographie est utilisée dans les civilisations sous différents formats depuis des milliers d’années. Des anciens Égyptiens à l’Internet moderne, l’utilisation de la cryptographie pour crypter et décrypter les messages est un outil essentiel de communication.
La cryptographie RSA (l’algorithme RSA pour être exact) est l’algorithme de cryptage asymétrique le plus omniprésent au monde. Rendu possible grâce à un certain nombre de percées cryptographiques et mathématiques, quiconque utilise Internet utilise la cryptographie RSA sous une forme ou une autre..

La plupart des crypto-monnaies utilisent un type de cryptage asymétrique similaire à RSA, connu sous le nom de cryptographie à courbe elliptique. Bien que différents, ils sont tous deux fondés sur des concepts similaires et la compréhension du RSA est importante pour approfondir la compréhension de la cryptographie utilisée dans les réseaux de crypto-monnaie..
Contents
Contexte cryptographique et cryptographie symétrique vs asymétrique
Jusque dans les années 1970, la cryptographie reposait principalement sur l’utilisation de clés symétriques. Dans les algorithmes à clé symétrique, deux utilisateurs qui souhaitent communiquer un message entre eux utilisent les mêmes clés cryptographiques à la fois pour le cryptage du texte en clair et le décryptage du texte chiffré. Les clés représentent un secret partagé entre les deux parties et peuvent être utilisées comme une forme de communication privée. Cependant, il existe certains problèmes inhérents à cette conception qui entraînent de graves inconvénients de son utilisation..
Par exemple, les deux parties doivent connaître la clé secrète afin de crypter et de décrypter le message. En dehors de la réunion en personne pour échanger ces informations, une surcharge de communication importante est nécessaire pour accomplir cela en privé via des supports qui ne sont pas sécurisés. Les tiers qui regardent ces chaînes peuvent être en mesure d’obtenir la clé secrète et ainsi, la méthode de cryptage est compromise. En outre, le concept de cryptage à clé symétrique n’est pas évolutif. Si vous souhaitez envoyer des messages cryptés à plusieurs personnes, vous devez mémoriser une clé secrète pour chacune de ces lignes de communication. De toute évidence, cela devient rapidement gênant et n’est clairement pas le meilleur modèle à utiliser par les réseaux de crypto-monnaie où la valeur est échangée.
La solution à ce problème est venue sous la forme de ce que l’on appelle le cryptage asymétrique, ou plus communément appelé cryptographie à clé publique. Le chiffrement asymétrique utilise deux clés, une clé publique et une clé privée. Dans la forme la plus basique de ce modèle, un utilisateur peut publier une clé publique, avec laquelle toute autre personne peut utiliser pour envoyer à cette personne un message chiffré et seule la personne qui a publié la clé publique et qui possède la clé privée correspondante peut déchiffrer et afficher ce message. L’utilisation d’une clé annule l’utilisation de l’autre et les clés ne doivent pas être échangées entre les parties qui souhaitent communiquer.
Le modèle de cryptage asymétrique a été rendu possible par 2 principes brillants issus d’une percée du mathématicien britannique James Ellis en 1970. Ellis a décrit une idée selon laquelle le cryptage et le décryptage sont des opérations inverses l’une de l’autre basées sur 2 clés différentes.

James Ellis, image de Le télégraphe.
Le concept est généralement représenté par un cadenas et une clé, le cadenas représentant la clé publique et la clé représentant la clé privée. Afin de mettre en pratique cette théorie, deux principes ont évolué.
La fonction Trapdoor
Une fonction de trappe est un concept très important en cryptographie où il est trivial de passer d’un état à un autre, mais calculer dans la direction opposée en retournant à l’état d’origine devient irréalisable sans information spéciale, connue sous le nom de «trappe».
La fonction de trappe la plus connue aujourd’hui, qui est la base de la cryptographie RSA, est appelée Factorisation principale. Essentiellement, la factorisation des nombres premiers (également appelée factorisation des nombres entiers) est le concept de la théorie des nombres selon lequel les entiers composites peuvent être décomposés en entiers plus petits. Tous les nombres composites (nombres non premiers) qui sont décomposés à leur plus élémentaire sont composés de nombres premiers. Ce processus est connu sous le nom de factorisation principale et a de graves implications lorsqu’il est appliqué à la cryptographie.
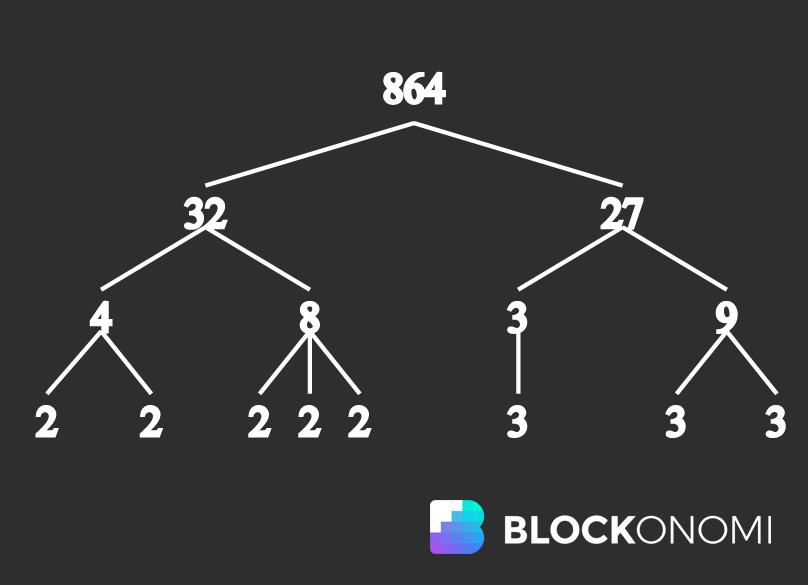
Factorisation Prime, Image utilisée à partir de Wikipédia
Essentiellement, la factorisation des nombres premiers extrêmement grands devient impossible à calculer en raison de la quantité d’essais et d’erreurs nécessaires pour réussir à factoriser le nombre en ses composants les plus élémentaires. Actuellement, aucun algorithme de factorisation efficace n’existe pour effectuer cette opération.
RSA et la façon dont il utilise la factorisation prime est décrit dans une section ultérieure, mais nous devons d’abord comprendre l’échange de clés Diffie-Hellman.
L’échange de clés Diffie-Hellman
L’échange de clés Diffie-Hellman est l’un des premiers protocoles de cryptographie à clé publique et permet fondamentalement d’échanger des clés cryptographiques sur un support public, en toute sécurité. Par souci de simplicité, tenter de conceptualiser l’échange de clés Diffie-Hellman et la section suivante sur le fonctionnement de l’algorithme RSA est beaucoup plus trivial avec des concepts abstraits par rapport aux mathématiques pures, nous n’appliquerons donc les mathématiques que lorsque cela est nécessaire..
L’exemple le plus courant utilisé pour conceptualiser l’échange de clés Diffie-Hellman est connu sous le nom d’échange de couleurs secrètes..
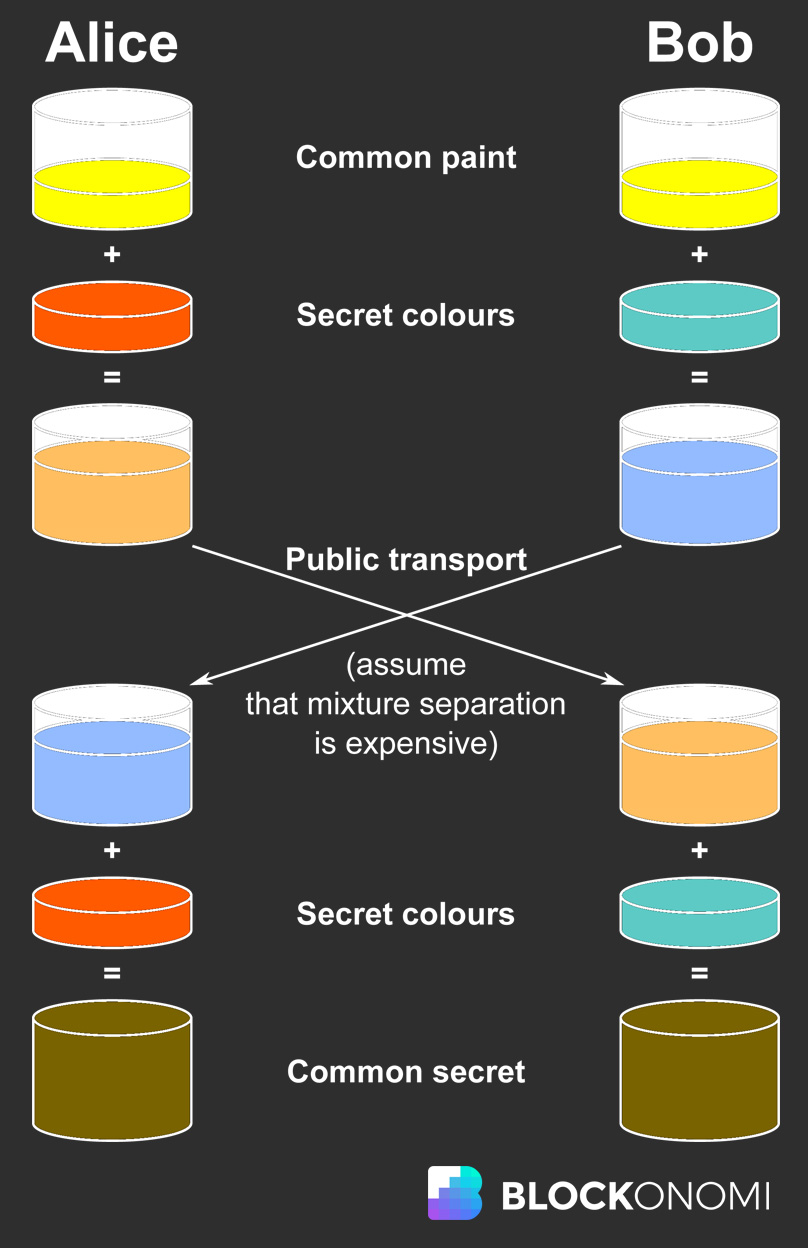
Échange de clés Diffie-Helman, image utilisée à partir de Wikipédia
L’image ci-dessus représente une ligne de communication entre Alice et Bob sur une chaîne publique où Eve peut écouter tout ce qui est communiqué publiquement entre Alice et Bob. Alors, comment Alice et Bob peuvent-ils communiquer un message privé en utilisant un cryptage asymétrique sans échanger explicitement ces informations sur le support public?
Ils échangent des informations secrètes entre eux sans réellement les partager. Le processus fonctionne comme suit:
Étape 1
- Alice et Bob conviennent que le jaune est la peinture commune à utiliser. Ces informations sont diffusées sur la chaîne publique pour qu’Eve le sache également.
- Le jaune représente la clé publique.
- Alice décide secrètement qu’elle va également utiliser Bleu avec Jaune et Bob décide secrètement qu’il va utiliser Rouge avec Jaune.
- Le bleu utilisé par Alice et le rouge utilisé par Bob représentent leurs clés secrètes.
Étape 2
- Ensuite, Alice et Bob mélangent leurs couleurs secrètes avec du jaune pour créer une couleur composite.
- Le mix d’Alice crée Green et le mix de Bob crée Orange.
- Maintenant, Alice et Bob s’envoient leurs couleurs composites.
- Eve reçoit également ces couleurs mais fait face à un problème, ces couleurs composites représentent une fonction de trappe.
- Il est facile de combiner deux couleurs pour en faire une troisième, mais il est impossible de l’inverser. Il est très difficile de déterminer quelles couleurs ont été utilisées pour créer la troisième couleur en n’ayant que la troisième couleur et le jaune d’origine.
Étape 3
- Alice et Bob mélangent ensuite leurs couleurs secrètes avec les couleurs composites reçues, ce qui donne les résultats suivants.
- Alice mélange le bleu avec l’orange composite de Bob.
- Bob mélange le rouge avec le vert composite d’Alice.
- Les deux mélanges donnent du brun.
C’est le secret de l’échange de clés Diffie-Hellman. Même si Alice et Bob se sont retrouvés avec Brown, ils n’ont jamais réellement échangé cette couleur, et Eve se retrouve sans les informations nécessaires sur les couleurs secrètes pour pouvoir calculer le message secret (Brown).
L’exemple ci-dessus est une visualisation très simple du fonctionnement de l’échange. Avec les mathématiques appliquées, la sécurité et l’intégrité des messages peuvent être assurées grâce à la cryptographie RSA en utilisant la factorisation principale comme trappe.
Comment fonctionne l’algorithme RSA?
L’algorithme RSA fonctionne en utilisant la trappe de factorisation principale et l’échange de clés Diffie-Hellman pour obtenir un cryptage asymétrique. Fondamentalement, la cryptographie RSA repose sur la difficulté de la factorisation principale comme méthode de sécurité. En utilisant un exemple très simplifié avec des mathématiques limitées décrites, l’algorithme RSA contient 4 étapes.
- Génération de clé – Au cours de cette étape, un utilisateur peut utiliser un générateur de nombres aléatoires ou simplement choisir 2 très grands nombres premiers (appelés p et q). Ces chiffres doivent être tenus secrets. Calculez n = pq où «n» est le module pour les clés publiques et privées et sa longueur est appelée longueur de clé. Rendre «n» public. Pour des tailles de clé égales ou supérieures à 1024 bits, il n’y a pas de méthode efficace pour résoudre cet algorithme (factoriser le très grand nombre «n») de manière efficace. Même le plus grand supercalculateur du monde prendrait des milliers d’années pour le résoudre. Ceci est connu sous le nom de problème RSA, et s’il est résolu, il compromettrait tous les cryptosystèmes basés sur RSA.
- Distribution de clés – Bob veut envoyer des informations secrètes à Alice afin que les étapes suivantes se produisent.
- Bob doit connaître la clé publique d’Alice pour chiffrer le message.
- Alice doit connaître sa clé privée pour déchiffrer le message.
- Pour que Bob puisse envoyer son message chiffré, Alice envoie sa clé publique à Bob.
- Alice ne distribue jamais sa clé privée.
Une explication plus approfondie des opérations mathématiques utilisées dans RSA peut être trouvée ici, mais sort du cadre de cet article.
De plus, le cryptage RSA permet la signature numérique des messages, ce qui est primordial pour les crypto-monnaies et est un élément clé du modèle de transaction UTXO de Bitcoin. Alice peut signer numériquement un message à Bob pour vérifier qu’elle l’a envoyé (en validant que sa clé privée a été utilisée) en produisant une valeur de hachage du message et en la joignant au message. Cette valeur peut être vérifiée par Bob qui utilise le même algorithme de hachage conjointement avec la clé publique d’Alice et compare la valeur de hachage résultante avec la valeur de hachage réelle du message.
Conclusion
Le cryptage RSA est la méthode de cryptage asymétrique la plus largement utilisée dans le monde en raison de sa capacité à fournir un niveau de cryptage élevé sans qu’aucun algorithme connu ne soit encore en mesure de le résoudre. Basé sur de brillantes percées en cryptographie et en mathématiques, notamment la fonction Diffie-Hellman Key Exchange et la fonction de trappe, le cryptage RSA est devenu primordial pour sécuriser les communications à travers le monde..


